Support Vector Machine
Contents
- Introduction
- Margin
- Objective Function of SVM
- The Lagrangian Multiplier Method and KKT Condition
- Final Solution
Introduction
“Nothing is more practical than a good theory.”
-Vladimir Vapnik
클로드 섀넌 등 위대한 석학들이 거쳐간 벨 연구소에서 (그 당시의) 머신러닝 분류기법의 4번타자인 Support Vector Machine 이 1995년 블라디미르 바프닉의 연구 끝에 탄생했다. Computational Complexity 에 대한 한계가 명확한 신경망을 제치고 SVM 은 효과적인 모델로 자리잡았다. 고차원에서 좋은 성능을 보이고, 샘플 수 보다 차원 수가 높아도 준수한 성늘을 보이고, 본질적으로 Computational Complexity 가 낮은 SVM 에 대한 연구는 계속되었다. 하지만 SVM 을 완성시킨 바프닉이 말한 것 처럼 2000년대 이후 SVM은 신경망을 뛰어넘지 못했고, 딥러닝이 대세가 된 현재 SVM 의 practical application 은 찾기 힘들다. 그렇다고 SVM 을 고대의 유물취급하기엔 kernel trick 등 효과적인 이론들을 머신러닝에 도입시켰고, ‘근본’ 모델 중 하나이기에 배울 수 있는게 많다. 바프닉의 말처럼 좋은 이론만큼 실용적인 것은 없기 때문이다.
SVM 은 classification 과 regression 에 쓸 수 있는 모델이지만, 대부분 classification 문제에서 사용된다. SVM 은 3가지의 경우에 따라 나뉘는데,
- Linear SVM for linearly seperable cases → Hard Margin SVM
- Linear SVM for linearly nonseperable cases → Soft Margin SVM
- Kernel methods for Nonlinear Classification
이번 포스팅은 SVM의 전반적 개요와 Hard Margin SVM 을 다룬다.
Margin
기존 딥러닝을 괴롭히는 고질병같은 overfitting 은 training data 의 성능이 과도하게 좋으면 일어난다. 이런 overfiited model 은 미래 데이터에 대한 예측이 떨어지기에, generalization 을 챙겨야한다. Overfitting 과 generalization ability 간의 tradeoff 에 대한 연구는 신경망쪽에서 활발하지만, SVM은 본질적으로 statistical learning theory 에 기반해 있기 때문에 train error 이 줄어들면 test error 도 줄어드는 모델이다.
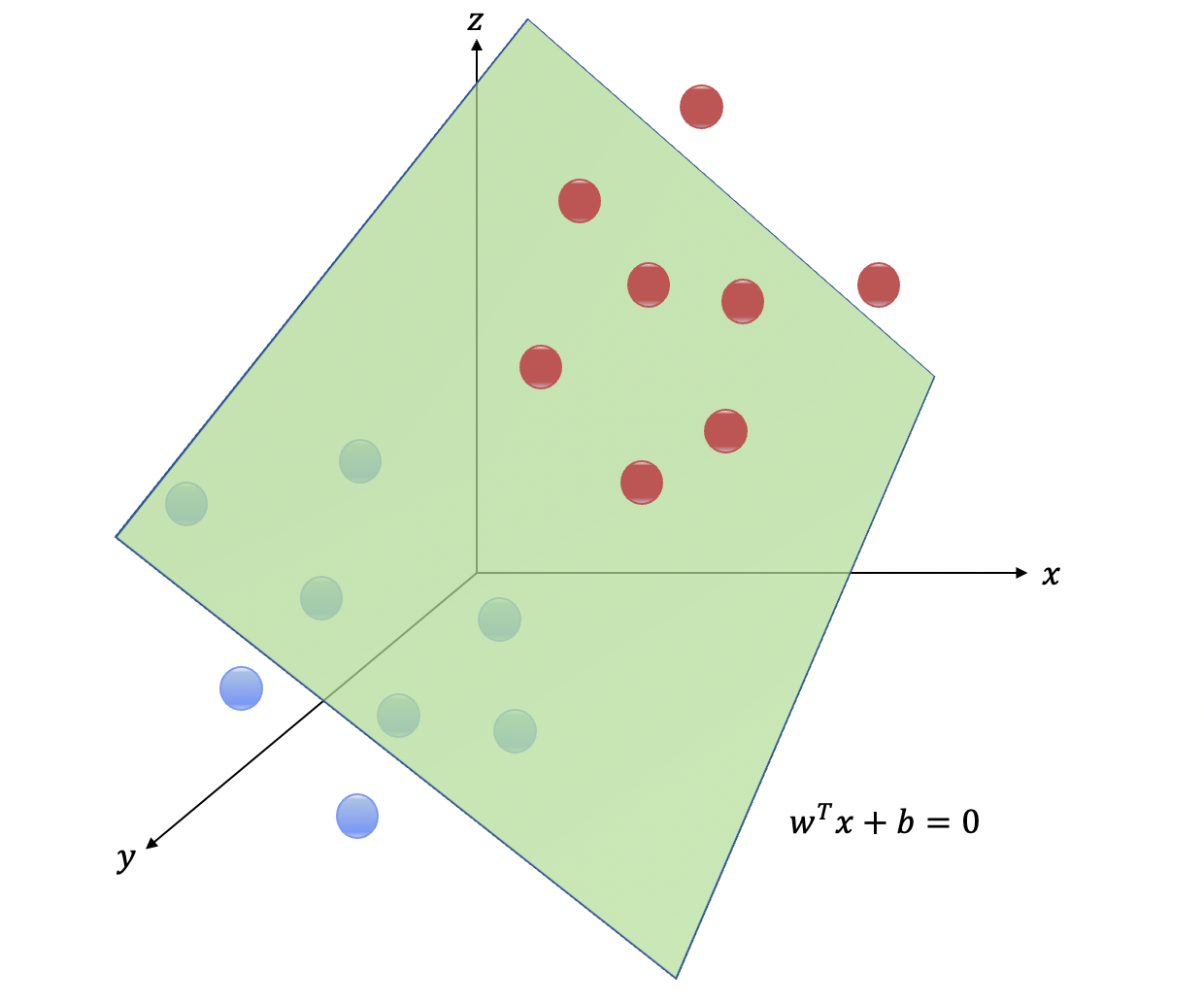
2개의 class 를 완벽히 분류하는 hyperplane 은 \(w^T + b = 0\) 이며, \(w\)는 hyperplane 의 법선벡터, \(b\)는 bias 다. \(w\)는 우리가 흔히 알고 있는 hyperplane 의 기울기, \(b\)는 hyperplane 의 y-intercept 라고 생각하면 간단하다.
본질적으로 \(N\)차원의 data point 들을 정확히 분류하는 hyperplane 을 찾는 것을 SVM 을 학습시킨다 라고 한다. 그렇기 때문에 \(w, b\)를 찾는 것이 궁극적인 목표다. 하지만 feature space 위의 데이터포인트들을 보면 두개의 클라스를 분류하는 hyperplane 은 여러개 일 수 있다. 잊지 말아야 할 것은 어느 머신러닝 모델과 다름없이 hyperplane 을 찾는것은 주어진 training data 를 통해 학습을 시키는 것이기에, training data 를 완벽히 분류할 수 있는 hyperplane 이 많이 존재하더라도 미래에 들어올 데이터도 잘 분류하는 최적의 hyperplane 을 찾는것이 관건이다. 이를 우리는 margin 이라는 개념을 도입해서 풀 수 있다.
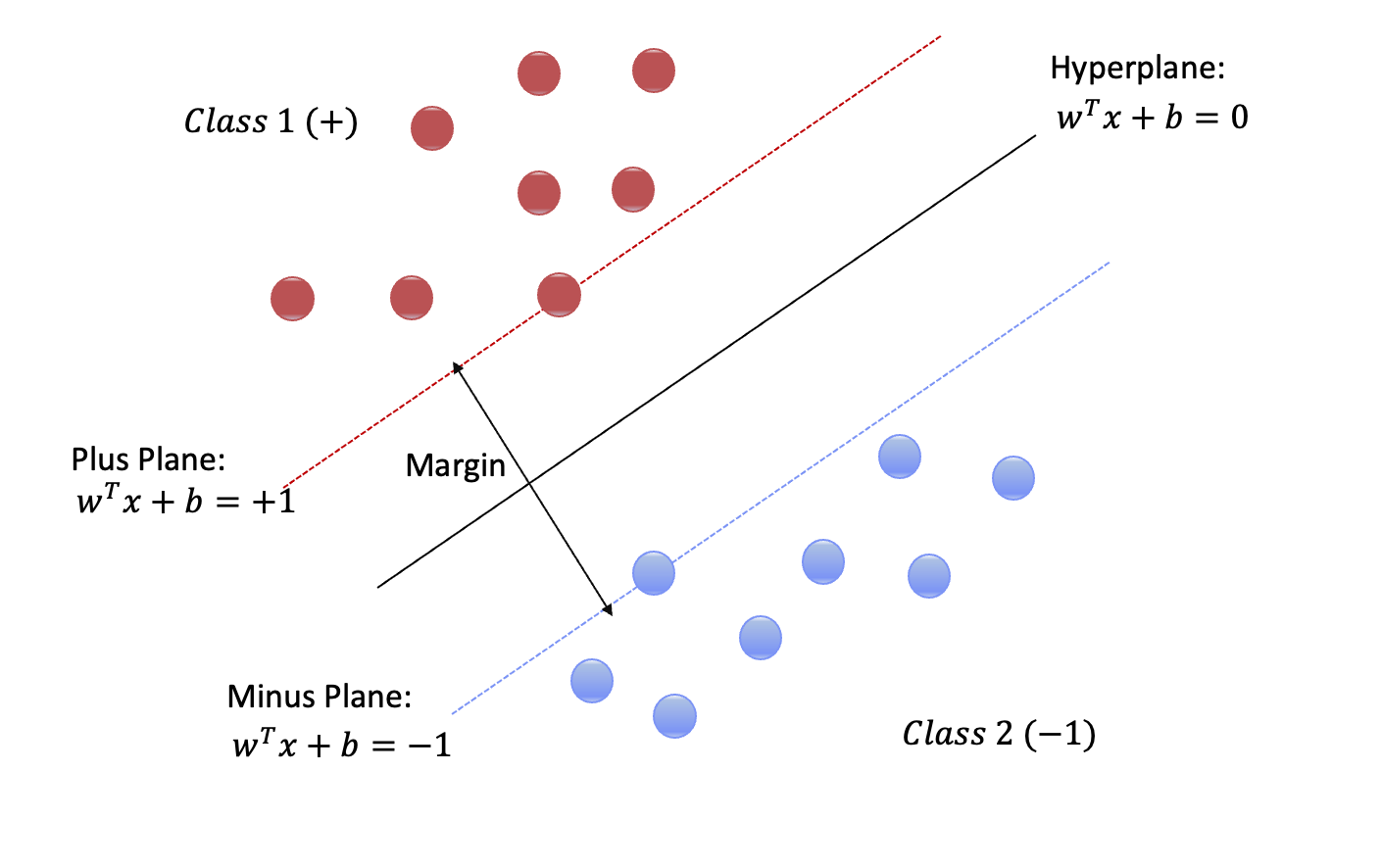
위 그림을 보면 두개의 클래스를 잘 구분하는 hyperplane 이 있다. 각 클래스에서 Hyperplane 과 가장 가까운 점들이 있고, 해당 점들은 또 다른 점선에 놓여있다. 해당 점선들을 각각 plus plane, minus plane 이라 부르며 이 두 plane 의 거리를 margin 이라 한다. Margin 이 클수록 두 클래스는 더 멀리 떨어져 있다는 것을 의미하며, 해당 training set 에서 margin 이 제일 큰 hyperplane 을 찾으면 미래 데이터도 잘 구분할 수 있다는 것을 의미한다. SVM의 목적은 이 margin 을 최대화 하는 hyperplane 을 찾는 것이다. hyperplane 의 \(w\) 가 법선벡터임을 여기서 알 수 있다.
Objective Function of SVM
SVM의 목적은 margin 을 최대화하는 hyperplane 을 찾는 것이다. 이를 수식으로 표현하는 과정은 복잡해 보이지만, 생각보다 간단하다. Plus plane 위의 점을 \(x^+\), minus plane 위의 점을 \(x^-\) 라고 부르겠다. 이때 \(w\)는 hyperplane 과 법선벡터이기 때문에 \(x^+\)과 \(x^-\) 를 평행이동관계로 표현 할 수 있다.
\[x^+ = x^- + \lambda w\]위 식은 최적화에서의 Basic Search Scheme 과 동일한 개념이다. \(x^-\)를 \(w\) 방향으로 \(\lambda\) 만큼 이동시키면 \(x^+\) 가 된다는 것을 의미한다.
이쯤에서 다시 목적이 뭔지 복습하는것이 좋다.
Training data 가 주어졌을 때 두개의 클래스를 구분하는 hyperplane 을 찾으려 한다.
SVM 에서는 margin 을 최대화 한다면 최적의 hyperplane 을 찾을 수 있다.
Margin 을 최대화하는 hyperplane 을 찾으려 한다. 그렇다면 margin 을 계산 가능한 식으로 유도해야 하는데, 위 평행이동관계식으로 margin 을 \(w\)로 표현 할 수가 있다. 먼저 \(\lambda\)를 \(w\)로만 표현하면 다음과 같다.
\[x^+ = x^- + \lambda w\\\\ w^Tx^+ + b = 1\\ w^T(x^-+\lambda w)+b=1\\ w^Tx^-+b+\lambda w^Tw = 1\\ -1 + \lambda w^Tw = 1\\\\ \lambda = \frac 2 {w^Tw}\]| 수식 | 설명 |
|---|---|
| \(x^+ = x^- + \lambda w\) | \(x^+, x^-\)의 평행이동관계 |
| \(w^Tx^+ + b = 1\) | plus plane |
| \(w^T(x^-+\lambda w)+b=1\) | plus plane 에 평행이동관계의 \(x^+\) 대입 |
| \(w^Tx^-+b+\lambda w^Tw = 1\) | 분배법칙 |
| \(-1 + \lambda w^Tw = 1\) | \(w^Tx^-+b = -1\) (minus plane) 치환 |
| \(\lambda = \frac 2 {w^Tw}\) | \(\lambda\) 로 정리 |
그 다음 Margin 자체를 유도해야 한다. Margin 은 \(x^+, x^-\) 사이의 거리이기 때문에 L2 norm 으로 전개를 할 수 있다.
\[margin = ||x^+ - x^-||_2\\ =||x^- + \lambda w - x^-||_2\\ =||\lambda w||_2\\ =\lambda \sqrt{w^Tw}\\\]Margin 을 전개한 식 \(\lambda \sqrt{w^Tw}\) 에 평행이동관계식에서 도출한 \(\lambda = \frac 2 {w^Tw}\)을 대입하면 다음과 같다.
\[margin = \frac 2 {w^Tw} \sqrt{w^Tw}\\ = \frac 2 {\sqrt {w^Tw}}\\ = \frac 2 {||w||_2}\]| SVM의 목적은 $$\frac 2 { | w | _2}$$ 를 최대화 하는걸로 귀결된다. 이 최대화 문제에 역수를 취해 최소화 문제로 만들면 다음과 같다. |
기존 문제에 역수를 취해 \(min\) 문제로 만든 뒤 L2 norm 의 제곱근을 없애기 위해 목적식에 제곱을 취해주면 \(w\) 로 표현한 SVM 의 목적식을 얻을 수 있다.
\[min \ \frac 1 2 \mid\mid w \mid\mid ^2_2 \rightarrow Objective \ function\]

목적식을 구했다면 제약식을 구할 차례다. SVM 에 새로운 데이터 포인트가 들어온다고 생각해보자. 그렇다면 해당 데이터포인트는 \(+1, -1\) 둘 중 하나의 클라스로 구분 될 것이고, \(+1\)이라면 plus plane 보다 위에 있을 것이고 \(-1\)이라면 minus plane 보다 아래에 있을 것이다. 데이터포인트의 클라스 (혹은 정답 레이블) 는 \(y_i\) 로 표현을 한다면, 위 제약식을 수식으로 쓰면 다음과 같다.
\[y_i(w^Tx_i+b)\geq 1, i=1,2,...n \rightarrow Constraints\]
이렇게 SVM 의 목적식과 제약식을 구할 수 있다 (편의상 Original Problem 이라 부르겠다).
Original Problem
\[\min \ \frac 1 2 \mid\mid w \mid\mid ^2_2 \rightarrow Objective \ function\] \[s.t \ y_i(w^Tx_i+b)\geq 1, i=1,2,...n \rightarrow Constraints\]
목적식의 변수 \(w\) 에 제곱이 붙어있고, 제약식은 linear 하다. 이렇게 SVM을 최적화에서 그토록 많이 배운 2차계획법 (Quadratic Programming, QP) 문제로 유도한 것이다. 이런 minimizing QP 문제는 convex optimization 이기 때문에, 전역최적해 (Global Minimum) 이 존재한다. 즉, 목적식을 최소화하는 \(w,b\) 가 단 하나만 존재한다는 뜻이다.
Lagrangian Multiplier Method and KKT Condition
SVM 의 Original Problem 은 QP 문제다. QP 문제는 전역최적해가 하나여서 다른 heuristics 가 필요 없다는 점에서는 좋지만, 제약식이 있는 최적화 문제는 추가 단계를 거처야만 풀 수 있다. 제약식이 연립방정식이면 라그랑주 승수법을 통해 새로운 최적화 문제를 풀어야 하고, 제약식이 연립부등식이면 KKT 조건이란 것을 만족하도록 유도해야 한다. SVM 의 Original Problem 을 유도하다 보면 라그랑주 승수법과 KKT 조건을 둘다 사용한다.
Lagrangian Multiplier Method
라그랑주 승수법이란 라그랑주 승수 (Lagrange Multiplier, 보조함수) 를 통해 제약 조건이 있는 최적화 문제를 풀기 위한 방법이다. SVM 의 경우엔 라그랑주 승수법은 제약식을 없애는 역할로 사용된다.
보통 라그랑주 승수는 \(\lambda\) 로 표현하는 경우가 많지만, 대부분의 소스와 예제에선 \(\alpha\) 를 사용한다.
기존 Original Problem 을 라그랑주 승수법을 통해 Lagrangian Primal 문제로 변환시키면 다음과 같다.
Original Problem
\[\min \ \frac 1 2 \mid\mid w \mid\mid^2_2 \rightarrow Objective \ function\] \[s.t \ y_i(w^Tx_i+b)\geq 1, i=1,2,...n \rightarrow Constraints\]
Lagrangian Primal
\[\max_\alpha\min_{w,b} \mathcal{L}(w,b,a) = \frac 1 2 \mid\mid w \mid\mid ^2_2 - \sum \alpha_i(y_i(w^Tx_i+b)-1) \rightarrow Objective \ function\] \[s.t \ \alpha_i \geq 0 \ , \ i=1,2,...,n \rightarrow Constraints\]
Original Problem 의 목적식과 제약식이 Lagrangian Primal 에선 \(\alpha\) 를 통해 하나의 목적식으로 합쳐졌고, 기존 제약식의 범위가 1보다 커야 했기 때문에 \(\alpha\) 가 0보다 커야 한다는 제약식이 생긴다. 이 Lagrangian Primal 문제의 목적식이 \(\max\min\) 이기 때문에, \(\max\) 만 존재하는 쌍대문제 (Dual) 로 바꿔 풀어야 한다. 즉, Primal formulation 을 minmize 후 Dual formulation 을 maximize 하면 된다.
Primal formulation 또한 Original Problem 과 같이 QP 이기 때문에 Convex 하고 Continuous 하다. 0에서 최솟값을 갖기 때문에 \(w, b\) 에 대해서 편미분을 해야한다.
\[\frac {\partial \mathcal{L}(w,b,\alpha_i)}{\partial w}=0 \rightarrow w = \sum^n_{i=1}\alpha_iy_ix_i\\ \frac {\partial \mathcal{L}(w,b,\alpha_i)}{\partial b}=0 \rightarrow \sum^n_{i=1}\alpha_iy_i=0\]이렇게 두가지 수식을 구할 수 있다. 되짚어보면 우리의 목적은 \(w, b\) 를 구하는 것이다. 첫번째 수식에 \(w\) 에 대한 정의가 있는데, \(\alpha\) 를 찾아야 하다. 그리고 두번째 수식에서 \(\alpha\) 와 \(y\) 의 곱의 합이 0이 되어야 한다는 것 또한 알게 되었다. 이 두가지 식을 다시 Primal formulation 에 대입을 하면 \(\alpha\) 값을 최대화 시키는것이 목적인 dual 문제로 변환시킬 수 있다.
Deriving Lagrangian Dual
Primal 을 Dual 로 바꾸는것은 어렵지 않다. 편미분을 통해 얻은 두 수식을 Primal 문제에 대입만 해주면 된다.
\[Primal: \min_{w,b} \mathcal{L}(w,b,a) = \frac 1 2 \mid\mid w \mid\mid ^2_2 - \sum \alpha_i(y_i(w^Tx_i+b)-1)\] \[w = \sum^n\_{i=1} \alpha_i y_i x_i\] \[\sum^n_{i=1} \alpha_i y_i=0\]
Primal 문제를 각 항별로 정리를 해보자.
| 수식 | 설명 |
|---|---|
| \(\frac 1 2 \mid\mid w \mid\mid ^2_2\) | Primal 첫째 항 |
| \(= \frac 1 2 w^Tw\) | L2 norm 벡터화 |
| \(= \frac 1 2 w^T \sum\alpha_jy_jx_j\) | \(w\)에 \(\sum^n_{i=1}\alpha_iy_ix_i\) 대입 |
| \(= \frac 1 2 \sum\alpha_jy_j(w^Tx_j)\) | \(w^T\)와 \(x_j\) 묶기 |
| \(= \frac 1 2 \sum \alpha_jy_j(\sum\alpha_iy_ix^T_ix_j)\) | \(w^T\)에 \(\sum^n_{i=1}\alpha_iy_ix_i\) 대입 |
| \(= \frac 1 2 \sum\sum\alpha_i \alpha_j y_i y_j x^T_i x_j\) | 전개 |
| 수식 | 설명 |
|---|---|
| \(-\sum \alpha_i(y_i(w^Tx_i+b)-1)\) | Primal 두번째 항 |
| \(= - \sum\alpha_iy_i(w^Tx_i+b)+\sum\alpha_i\) | 전개 |
| \(= - \sum\alpha_iy_iw^Tx_i-b\sum\alpha_iy_i+\sum\alpha_i\) | 전개 |
| \(= -\sum\sum \alpha_i \alpha_j y_i y_j x^T_i x_j + \sum \alpha_i\) | \(-b\sum\alpha_iy_i\) 는 0이기 때문에 삭제, \(w = \sum^n_{i=1}\alpha_iy_ix_i\) 대입 |
Primal 의 두 항을 정리한것을 합치면 다음과 같은 최종 Dual formulation 을 완성 시킬 수 있다.
Lagrangian Dual
\[\max_\alpha \sum^n_{i=1} \alpha_i - \frac 1 2 \sum^n_{i=1} \sum^n_{j=1} \alpha_i \alpha_j y_i y_j x^T_i x_j \rightarrow Objective \ function\] \[s.t \ \sum^n_{i=1}\alpha_i y_i = 0, \ \alpha_i \geq 0, \ i=1,2,...,n \rightarrow Constraints\]
위 Dual 문제도 Original Problem, Primal formulation 과 동일한 QP다. 그렇기 때문에 목적식을 만족시키는 \(\alpha\) 는 하나만 존재한다. \(\alpha\) 를 구하면 \(w = \sum^n_{i=1}\alpha_iy_ix_i\\\) 를 통해 \(w\) 를 구할 수 있다. 하지만 위에서 언급한 것 처럼 QP 문제에서 제약식이 연립부등식이면 KKT 조건을 만족시켜야 한다.
Karush-Kuhn-Tucker Conditions
일반적인 KKT 조건이라 하면 다음과 같은 3가지의 조건을 의미한다.
- 모든 독립변수에 대한 미분값은 0이다 - Stationary 조건
- 모든 라그랑주 승수와 제한조건 부등식의 곱은 0이다 - Primal Feasibility 조건
- 라그랑주 승수는 음수가 아니어야 한다 - Dual Feasibiliity 조건
SVM 의 겨우엔, \(w, b,a\) 가 Lagrangian dual 의 최적해가 되기 위해서 KKT 조건을 풀어쓰면 다음과 같이 수식화 할 수 있다.
- Stationary
$\frac {\partial \mathcal{L}(w,b,\alpha_i)}{\partial w}=0 \rightarrow w = \sum^n_{i=1}\alpha_iy_ix_i
\frac {\partial \mathcal{L}(w,b,\alpha_i)}{\partial b}=0 \rightarrow \sum^n_{i=1}\alpha_iy_i=0$
- Primal Feasibility
\[y_i(w^Tx_i+b)\geq 1, i=1,2,...n\]
- Dual Feasibility
\[\ \alpha_i \geq 0, \ i=1,2,...,n\]
- Complementary Slackness
\[\alpha_i(y_i(w^Tx_i+b)-1)=0\]
그런데 자세히 보면 첫 3가지 조건들은 익숙하다. Stationary 조건은 Lagrangian Primal 의 독립변수들을 편미분할때 사용했다. Primal Feasibility 는 Original Problem 의 제약식이고, Dual Feasibility 는 Lagrangian Primal 의 제약식이다. 이미 첫 3가지 KKT 조건을 염두에 두고 Dual Problem 을 유도한 것이다. 그렇기에 마지막 조건인 Complementary Slackness 를 통해 우리는 최종해를 구할 수 있다.
Final Solution
KKT의 첫번째 조건을 유도하는 과정에서 \(w = \sum^n\_{i=1}\alpha_iy_ix_i\) 를 통해 최종 해를 구할 수 있다는 것을 안다. \(x_i, y_i\) 는 학습데이터이기 때문에 \(\alpha_i\) 만 찾으면 된다. 이는 Complementary Slackness 를 통해 찾을 수 있다.
\[\alpha_i(y_i(w^Tx_i+b)-1)=0\]Complementary Slackness 조건을 보면 \(\alpha_i\) 와 \(y_i(w^Tx_i+b)-1\) 중 반드시 하나는 0의 값을 가져야 한다는 것을 알 수 있다. 그렇다면 두가지 경우를 생각 할 수 있다.
- \[\alpha_i > 0 \ and \ y_i(w^Tx_i+b)=1\]
- \[\alpha_i = 0 \ and \ y_i(w^Tx_i+b)-1\neq 0\]
첫번째 경우의 두번째 항목을 자세히 보면 margin 의 수식인 것을 알 수 있다. 이는 training set 의 \(x_i\) 가 plus plane 혹은 minus plane 위에 있다는 것을 의미하며, 해당 \(x_i\) 를 support vector 이라 부른다.
두번째 경우는 \(x_i\) 가 plus plane 혹은 minus plane 위에 있지 않다는 것을 의미한다. 그렇기 때문에 Hyperplane 을 구축하는데 있어서 영향을 미치지 않는다.
첫번째 경우에서 찾은 support vector 을 찾으면 margin 을 찾은 것과 다름없다. 왜냐하면 support vector들로 plus plane, minus plane 을 구할 수 있으며 최종적으로 두 Plane 간의 거리가 maximum margin 이기 때문이다.