Orthogonality of Functions, Fourier Transformation and the Sampling Theorem (Audio Signal Processing Pt.1)
Contents
-
Orthogonality of Functions
-
Fourier Transformation
-
Waveforms and Sampling Theorem
Orthogonality of Functions
우리는 벡터를 선형대수학적 관점에서 나오는 방향과 값을 갖는 수학적 개체 라고 처음 배운다. 하지만 함수 (Function) 도 벡터처럼 다룰 수 있다. 함수를 벡터처럼 다룬다는 것이 와닿지 않을 수도 있지만, 벡터의 성질을 그대로 함수에 대입해보면 얼핏 감을 잡을 수 있다. 함수를 벡터처럼 다룰 때 세가지 정의를 짚고 넘어가야 한다.
Definition 1: 함수의 내적 (Inner Product)
\[(f_1,f_2)= \int_{a}^{b} {f_1}(x){f_2}^*(x) \,dx\]보통 벡터의 내적은 벡터의 방향이 얼마나 일치한지 (혹은 다른지) 를 알기 위한 용도로 쓰인다. 두가지 함수의 방향이 얼마나 일치하는지도 내적의 개념을 도입 할 수 있다.
Definition 2: 직교함수 (Orthogonal Functions)
\[(f_1,f_2)= \int_{a}^{b} {f_1}(x){f_2}^*(x) \,dx = 0\]\(a\)부터 \(b\) 구간까지의 함수의 내적은 적분식으로 표현 할 수 있고, 이 내적의 값이 0이 될 때 두 함수 \(f_1, f_2\)는 직교한다 라고 표현 할 수 있다.
Definition 3: 직교집합 (Orthogonal Set)
\[(\phi_m,\phi_n)= \int_{a}^{b} {\phi_m}(x){\phi_n}^*(x) \,dx, for \ m \neq n\]\(\phi_m, \phi_n\) 이라는 실수함수의 집합이 같지 않다는 정의 하에 두 집합은 Orthogonal Set 이다. 이때, \(\phi_n\) 을 기저함수 (basis function) 이라고 부른다.
애초에 함수를 벡터의 성질로 표현한다는 것이 굉장히 추상적인 아이디어다. 이를 이해하기 위해 공부 중 마음에 들던 예시를 소개해보겠다.
선형대수학에서 벡터를 공부 할 때 벡터의 차원 이라는 표현을 쓰는데, 이걸 정의역과 치역의 관계로 생각하면 함수의 벡터화를 이해하는데 편하다.
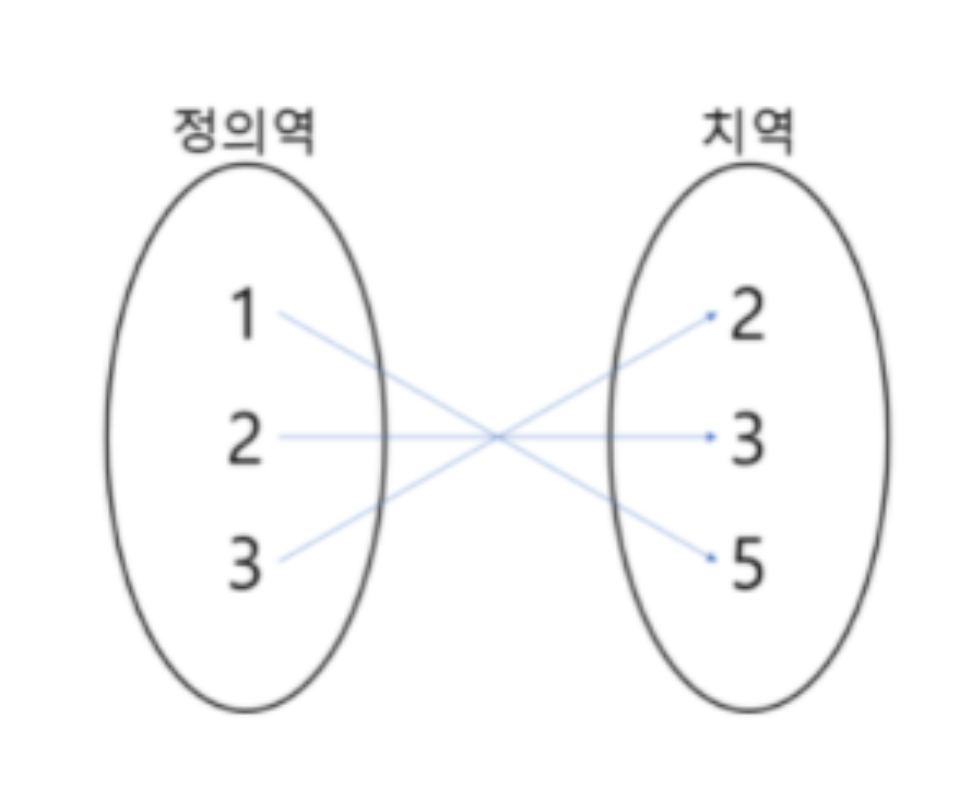
예를 들어 \(v = (5,3,2)\) 라는 벡터가 있는데, 이 벡터는 3차원 실수공간의 점이다. \(v \in \mathbb{R}\)
3차원 실수공간의 점이기 때문에 각 원소가 각 차원에 매핑 된 것이다. 즉 정의역인 1차원이 5라는 치역에 매핑, 2차원이 3이라는 치역에 매핑, 3차원이 2라는 치역에 매핑된 것이다. 함수를 벡터라고 생각 할 때 함수는 무한개의 실수를 정의역으로 삼고, 이 무한개의 실수는 무한개의 함수값, 즉 치역으로 매핑되는 것이다. 결국 함수는 구간이 명시되지 않는 이상 무한차원의 벡터라고 생각 할 수 있다.
선형대수학에서 나오는 개념 중 기저벡터 또한 있는데, 2차원의 벡터를 표현 할 때 \(\hat{i},\hat{j}\) 라는 기저벡터 두개의 선형결합으로 하나의 벡터를 표현 할 수 있다. \(n\)차원의 벡터를 기저벡터로 표현하고 싶으면 \(n\)개의 기저벡터가 필요 한 것이다. 이 개념을 함수에 대입하면, 함수는 무한차원의 벡터이기 때문에 무한개의 직교하는 기저함수가 필요하다.
\[f(x) = \sum_{n=0}^{\infty}{c_n}{\phi_n}(x)\]결론적으로 상수 \(c\) 와 기저함수 \(\phi\) 로 함수를 표현 할 수 있게 되는 것이다. 이 개념들이 푸리에급수의 핵심이 된다.
Fourier Transformation
푸리에 변환을 논하기 전에 시그널이 무엇인지 짚고 넘어가야 한다. Signal(신호) 는 같은 형태를 반복하는 주기를 갖는 파동 이고, 시간축에 정의된 음성(audio), 전파(electric wave) 일수도 있고, 공간축에 정의된 이미지 일 수도 있다 (이미지도 신호다 어렵다). 음성 시그널, 대표적으로 speech (목소리 시그널) 은 공기 분자가 진동하면서 \(x\)축을 시간, \(y\)축을 amplitude 로 매핑 할 수 있다.
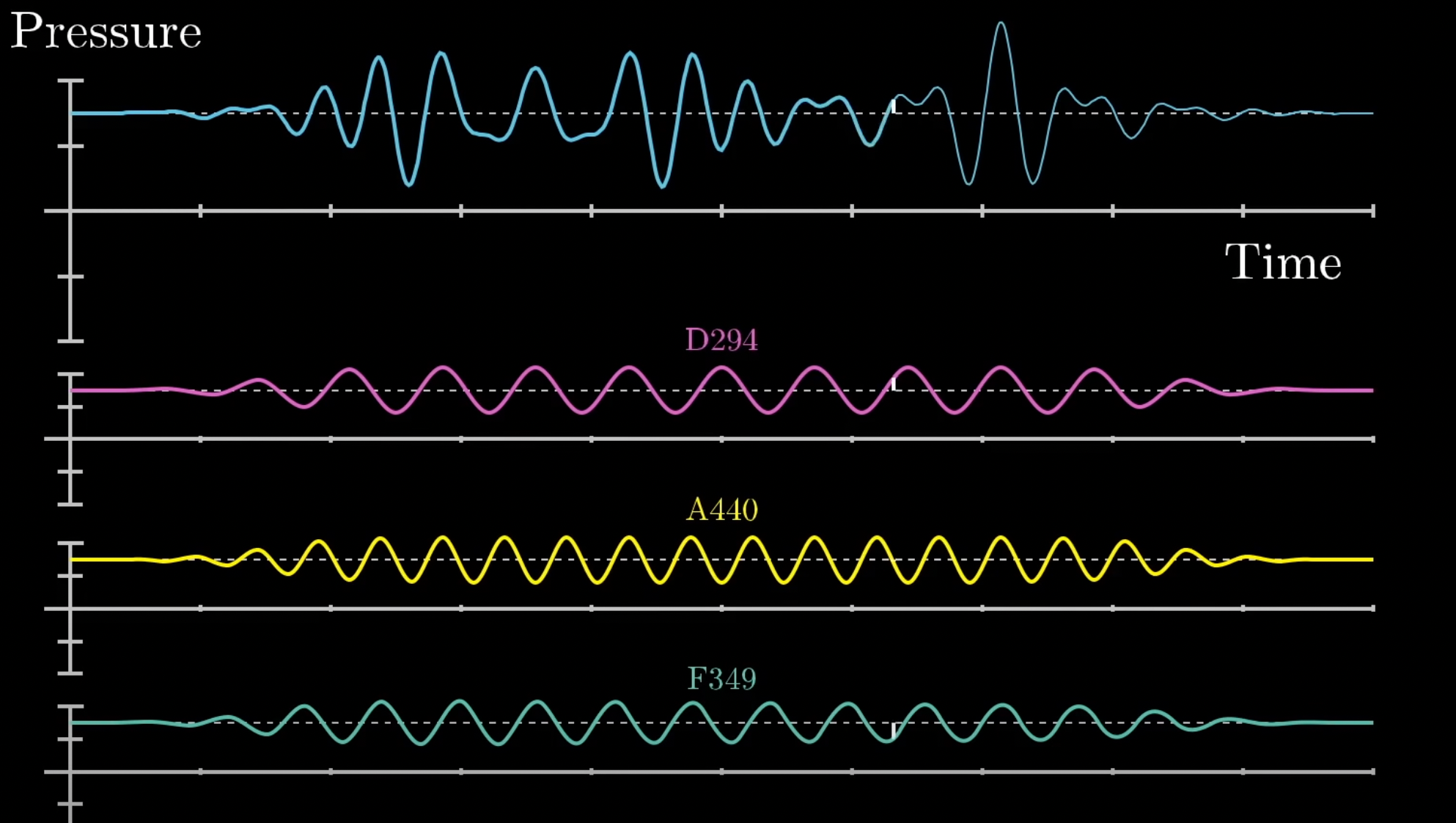
그런데 이런 시그널은 굉장히 많은 주파수들이 섞여있다. 당장 핸드폰으로 음성메모 앱을 켜서 목소리를 녹음해보면 그려지는 시그널은 아무리봐도 정현파가 아니다. 이는 하나의 목소리 시그널에 다양한 주파수들이 섞여있기 때문인데, 정확히 어떤 성분들이 섞여있는지 한눈에 봐선 모른다. 이런 섞여 있는 시그널을 각각 주기함수들의 합으로 표현한 것이 바로 푸리에 변환이다.
앞서 설명한 것처럼 함수도 무한개의 직교함수의 합으로 표현 할 수 있기 때문에, 푸리에 변환은 이 직교함수를 주기함수 \(sin, cos\) 로 설정해서 복잡한 하나의 신호를 간단한 주기함수의 합 (급수)으로 표현한 것이다. 잘 보면 푸리에 변환은 그저 복잡한 하나의 시그널을 주기함수들로 분해해줄 뿐만 아니라, \(x\)축을 시간 영역에서 주파수 영역 - frequency domain 으로 매핑해준다.
Audio Signal 을 사용하는 통신분야에서는 시간축을 주파수 영역으로 매핑하고, Image 를 Signal 로 해석해서 사용하는 CV 분야에서는 공간축을 주파수 영역으로 매핑해서 사용한다.
Waveforms and Sampling Theorem
세상엔 해석하고 분석 할 수 있는 다양한 시그널들이 존재하지만, 오디오 시그널에 집중해보자. 오디오라는 것 자체가 공기분자를 매질로 이용한 진동인데, \(x\)축은 시간이고 \(y\)축은 Amplitude, 즉 진폭이다.
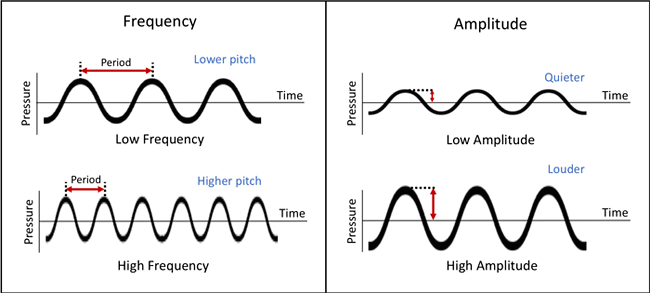
그래프를 보면 특정 지점에서 다음 등장하는 값까지 주기 (Period) 라고 하고, 1을 주기로 나눈 값을 주파수 (frequency) 라고 한다. 이때 주파수가 높을수록 (혹은 주기가 작을수록) 사람이 듣기엔 더 고음역대의 소리가 들리고, \(y\)축인 진폭이 클수록 사람이 듣기엔 소리가 크다 라고 느낀다.
우리가 소리의 척도로 사용하는 Decibel 이 진폭에서부터 derive 되지만, 완전히 선형관계는 아니고 진폭을 약간 변형시킨 값이다.
| Function | 설명 |
|---|---|
| \(x\)축 | Time |
| \(y\)축 | Amplitude |
| \(T\) | 주기 (Period) |
| \(f\) | 주파수 (Frequency). \(f=1/T\) |
이런 오디오 시그널은 연속적인 아날로그 신호인데, 이걸 컴퓨터에서 사용하고 분석하려면 디지털 신호로 변환시키는 과정을 거쳐야 한다. 이 과정을 ADC (Analog Digital Conversion) 이라고 한다. 연속적인 아날로그 시그널을 이산적인 디지털 신호로 변환시키는 ADC 에는 두 단계가 있다.
-
샘플링 (Sampling)
-
양자화 (Quantization)
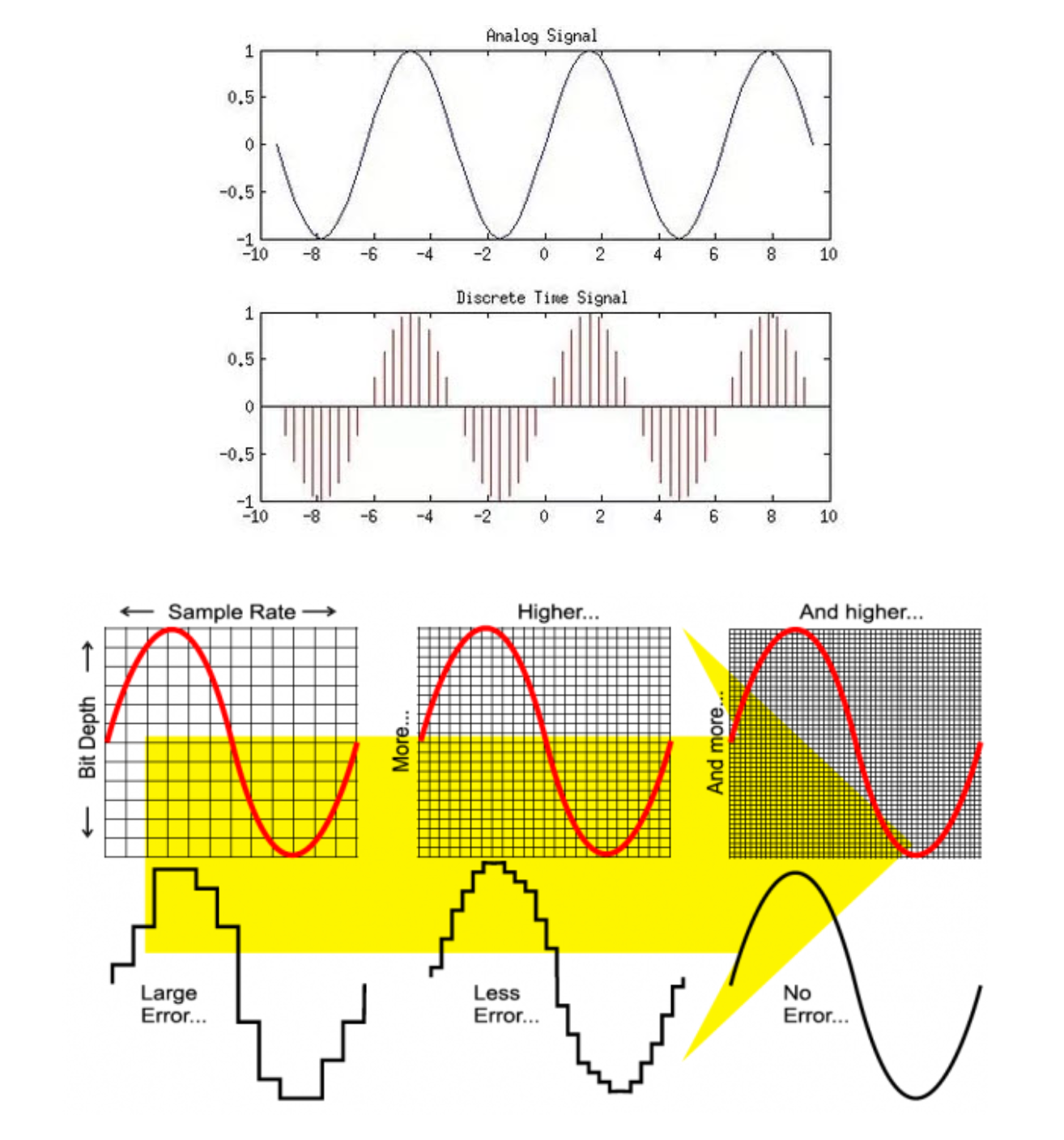
Sampling
샘플링은 아날로그 시그널에서 초당 몇개의 샘플을 추출하는 과정을 의미한다. 이를 Sample Rate 로 정하는데, 녹음 프로그램에서 Sample Rate 를 정할 때 기본값이 44.1k 인 것을 많이 봤을 것이다. 이 Sample Rate 는 아날로그 오디오 시그널을 초당 44,100 회 샘플링 한다는 것을 의미한다.
Quantization
양자화는 진폭을 어떤 이산적인 값으로 근사시키는 과정을 의미한다. 이를 bit depth 로 정하는데, 만약 bit depth 가 16이면 추출된 하나의 샘플의 진폭을 \(2^{16}\) 만큼 이진수로 근사시킨다는 것을 의미한다.
즉 그림에서 보는 것 처럼 이 아날로그 신호를 \(x\)축에서 얼마나 촘촘히 쪼개서 저장할지, 그리고 \(y\)축에서 얼마나 촘촘히 쪼개서 저장할지를 정하는 것이 각각 샘플링과 양자화다.
그런데 아날로그 신호를 디지털로 저장하면 어쩔 수 없이 정보의 손실이 일어날 수 밖에 없다. 아무리 샘플링과 양자화를 촘촘히 해도 연속값을 이산값으로 저장하는 과정이기 때문에 정보손실은 불가피하다. 이런 정보손실을 반증하는 이론이 바로 그 유명한 Nyquist Theorem 이다.
Nyquist Theorem
나이퀴스트 이론이란 하나의 오디오 시그널이 갖는 최고 주파수의 두배만큼 sampling rate 를 지정하면 정보의 손실은 없다 라고 증명해주는 법칙이다. 이 이론에 의거하여 logic pro 같은 녹음 프로그램에서 44.1k 의 sampling rate 를 사용하는지 알 수 있다. 사람의 가청 주파수의 범위는 2Hz ~ 20,000Hz 인데, 2만Hz 의 두배 + 오차 허용범위 10%를 Sampling Rate 로 지정한 것이다. 즉 음악을 녹음 할 때 Sample Rate 를 44.1k 로 지정해서 ADC 를 진행하면 사람이 음악을 들을 때 정보의 손실이 없다.