Ridge Regression, LASSO, and ElasticNet

Contents

• Introduction
• Ridge Regression
• LASSO: (Least Absolute Shrinkage and Selection Operator)
• Visualization of Ridge and LASSO
• ElasticNet

해당 포스트는 2021년 1학기 고려대학교 강필성 교수님의 ‘다변량분석’ 강의를 참고하여 작성되었습니다.

이미지는 강필성 교수님의 강의 슬라이드에서 발췌하였습니다.

A+ 감사했습니다 교수님

Introduction

이전 장에선 모델 외부에서 작동하는 알고리즘을 통해 차원축소를 진행하는 FS, BE, SS, Genetic Algorithm 에 대해 알아보았다. 이번 장에선 모델 내부, 정확히 말해서는 목적함수에 적은 수의 변수를 선호하도록 걸어두는 장치를 통해 차원축소를 하는 방법론에 대해 서술하고자 한다.

\[\hat y = \hat \beta_0 + \hat \beta_1x_1 + \hat\beta_2x_2+...+\hat\beta_dx_d\]

위 식은 다중선형회귀분석의 formulation 으로, 설명변수들과 회귀계수의 선형결합으로 표현된다. 이때 OLS 를 최소화 시키는 회귀계수를 찾는 것이 목적이며,

\[min\ {1 \over 2} \sum(y_i - \hat y_i)^2 = min\ {1 \over 2} \sum(y_i - \sum \hat\beta_jx_{ij})^2\]

OLS 의 식은 위와 같다. 이처럼 사용하는 회귀모델에 따라 적합한 목적식/cost function 이 존재하며, 대부분 이 목적식을 최소화 하는것이 목적이다. 이때 목적식들은 변수의 수에 따른 수정계수가 없기 때문에 자동으로 모든 설명변수를 사용하게 된다. 하지만 이번 장에서 알아보는 3가지 방법론에선 이 목적식에 새로운 항을 추가함으로써 목적식을 최소화하는데 있어 적은 수의 변수를 선호하도록 장치를 걸어둔다.

Ridge Regression

Ridge Regression 은 변수간 상관관계가 높은 데이터로 다중선형회귀분석의 회귀계수를 효율적으로 추정하기 위해 처음 고안되었다.

\[\lambda \sum^d_{j=1}\hat\beta^2_j\]

Ridge Regression 은 회귀모델의 목적식에 위와 같은 \(L_2 \ norm\) penalty 를 추가해 진행 할 수 있다. MLR 의 목적식인 min. OLS 의 경우엔, 목적식이 아래와 같이 변형된다.

\[min\ {1 \over 2} \sum(y_i - \sum \hat\beta_jx_{ij})^2 +\lambda \sum^d_{j=1}\hat\beta^2_j\]

\(\lambda\) 는 hyperparameter 로, 회귀계수 \(\hat \beta\) 의 제곱합의 가중치 역할을 한다. 다중선형회귀분석은 위 목적식의 최소화를 목적으로 두기 때문에, 만약 사용하는 성능평가지표 (ex. \(R^2\)) 값이 두 모델간 같다면 적은 \(\hat \beta\) 값을 선호하게 만드는 장치다. 이 penalty 는 MLR 의 목적식 뿐만 아니라, 모든 회귀모델의 목적식에 추가하여 사용할 수 있다.

Ridge Regression 이 과연 차원축소방법론인가? 를 물어본다면, 엄밀히 따지면 아니다. \(L_2 \ norm\) penalty 를 추가함으로써 특정 \(\hat \beta\) 값을 아주 작게 만들 수는 있지만, 0으로 수렴하도록, 즉 해당 변수를 사용하지 않도록 만드는 경우는 드물기 때문이다. 그렇기 때문에 Ridge Regression 은 차원축소 보단 변수간 상관관계가 높은 경우 regression 모델을 구축하는데 사용된다. 그렇기 때문에 Ridge Regression 은 Regularization method (정규화 방법론) 로 분류된다.

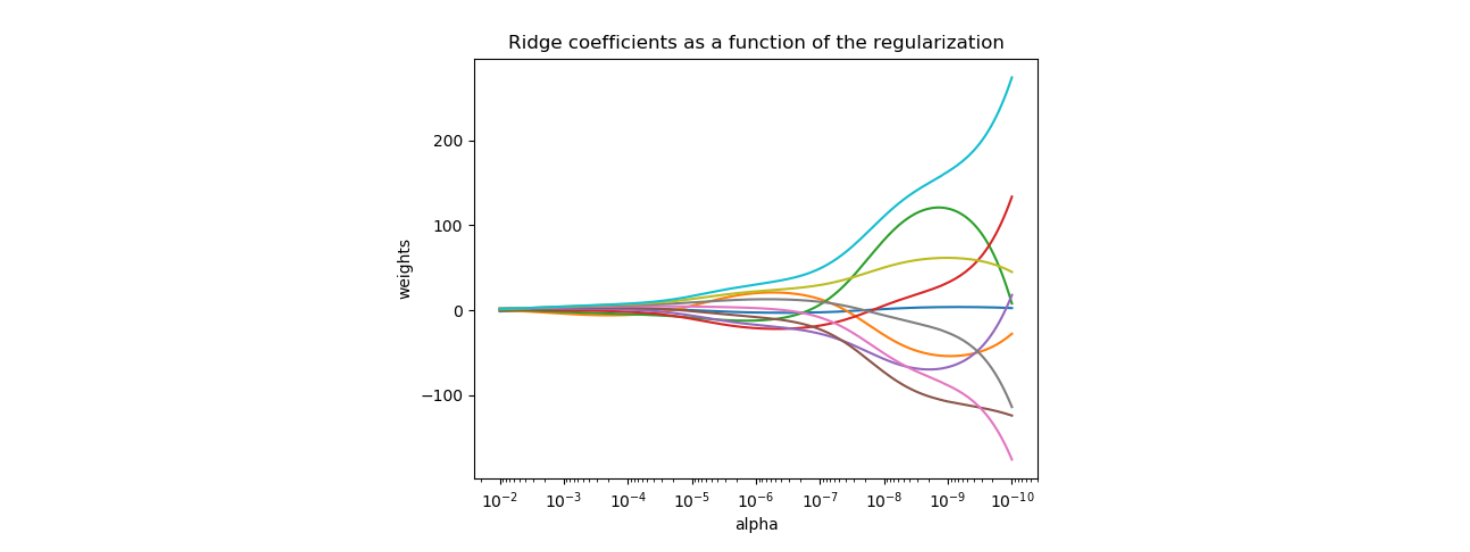
Hyperparameter \(\lambda\) 값에 따른 회귀계수 \(\hat \beta\) 값들의 변화량은 위 그래프를 통해 확인할 수 있다. 각 선이 하나의 설명변수와 선형결합하는 회귀계수이며, \(\lambda\) 값이 커질수록 (왼쪽으로 갈수록) 모든 회귀계수들이 0에 수렴하는 것을 볼 수 있다.

LASSO: (Least Absolute Shrinkage and Selection Operator)

LASSO (Least Absolute Shrinkage and Selection Operator) 은 이름에서 볼 수 있듯이 변수선택법, 즉 차원축소 방법론이다.

\[\lambda \sum^d_{j=1} \mid \hat\beta_j \mid\]

Ridge Regression 과는 달리, 회귀모델의 목적식에 \(L_1 \ norm\) penalty 를 추가하는 방법론이다. MLR 의 목적식인 min. OLS 의 경우엔, 목적식이 아래와 같이 변형된다.

\[min\ {1 \over 2} \sum(y_i - \sum \hat\beta_jx_{ij})^2 +\lambda \sum^d_{j=1} \mid \hat\beta_j \mid\]

Ridge Regression 에선 회귀계수를 아주 작게 만듬으로써 해당 설명변수의 영향을 적게 만든다면, LASSO 는 특정 회귀계수를 완전히 0으로 만들어 해당 설명변수를 제거한다. 즉, 제거되지 않은 변수가 선택된 것이다. Ridge Regression 처럼 동일한 hyperparameter 인 \(\lambda\) 가 있으며, \(\lambda\) 가 커질수록 제거되는 변수가 많아진다.

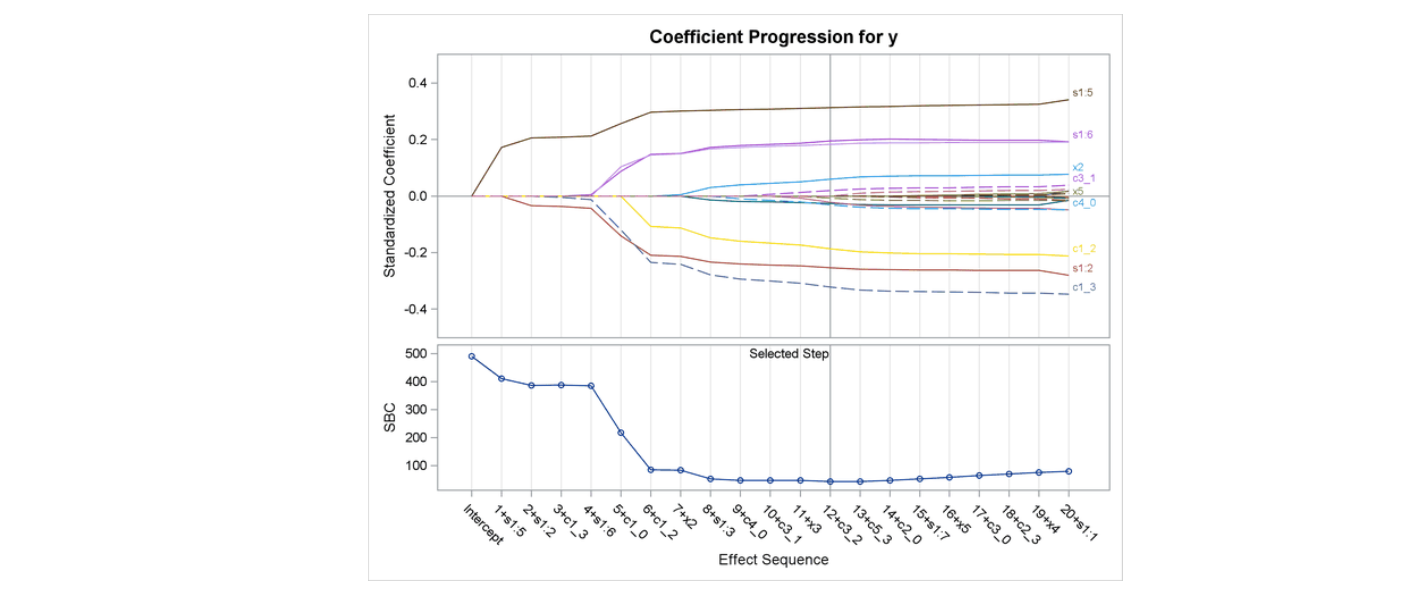
Ridge Regression 의 Regularization path 과는 달리, LASSO 의 Regularization path 를 보면 각 회귀계수가 \(\lambda\) 의 값이 커지면 (왼쪽으로 갈수록) 줄어들다가, 어느 순간부터 딱 0으로 수렴하는 것을 볼 수 있다.

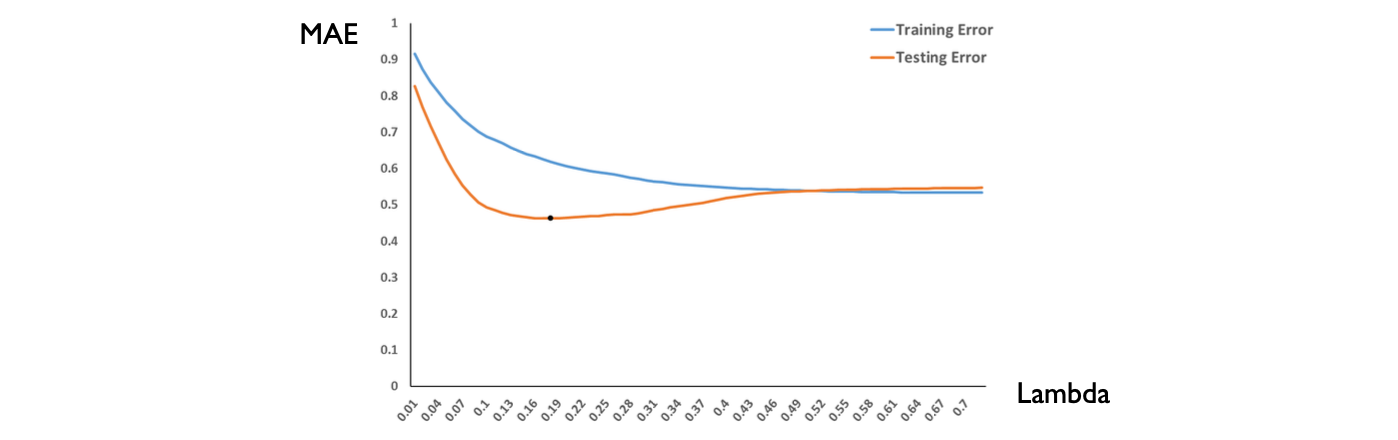
이때 \(\lambda\) 는 hyperparameter 로, 적당한 값을 찾아 최적의 모델 성능을 도출하는게 중요하다. 이때 보통 training set 과 test set 을 동시에 사용해서 \(\lambda\) 의 변화에 따른 성능평가지표를 구한 뒤, error 를 최소화 시키는 \(\lambda\) 값을 사용한다.

Visualization of Ridge and LASSO

Ridge Regression 과 LASSO 는 목적식에 각각 \(L_1, \ L_2 \ norm\) 을 추가하여 회귀계수의 값을 조정한다.

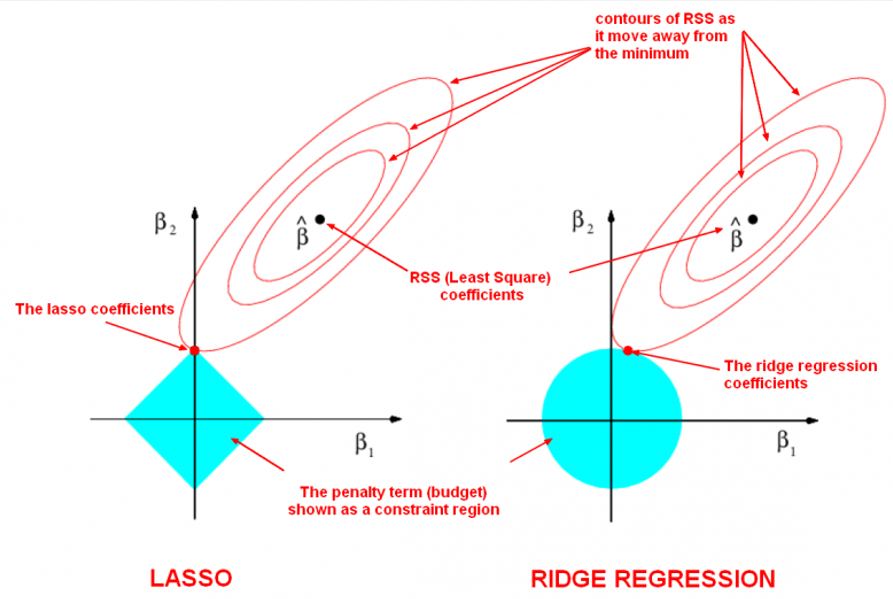
위 예시를 보면 두개의 변수를 사용한 회귀모델에 각각 Ridge, LASSO 를 사용한 시각화 모형이다. 붉은 등고선은 \(\hat \beta_1, \hat \beta_2\) 의 값의 변화에 따른 RSS (Least Square Coefficients) 값을 나타낸다. 이때 좌측 그림은 LASSO 의 \(L_1 \ norm\) penalty 를, 우측 그림은 Ridge 의 \(L_2 \ norm\) penalty 를 제약 region 으로 표현 한 것이다. 목적식에 각각 penalty 를 추가했기 때문에 등고선의 가장 낮은 부분이 적절한 \(\hat \beta_1, \hat \beta_2\) 로 선택 될 것이며, 이는 가장 밖에 있는 등고선과 penalty 영역이 만나는 지점이 된다.

그림을 자세히 보자. \(L_1 \ norm\) penalty 는 manhattan distance 이기 때문에 다이아몬드 형식으로 영역이 나타나기 때문에, 등고선과 영역이 만나는 부분은 \(\hat \beta_2\) 가 0이 되는 절편이다.\(\hat \beta_2\) 값이 0이 되었기 때문에, 이에 상응하는 \(x_2\) 변수가 선택되지 않는다.

반면 \(L_2 \ norm\) penalty 는 euclidean distance 이기 때문에 원으로 영역이 나타난다. 그렇기 때문에 등고선과 영역이 만나는 점으로 회귀계수가 결정나며, \(\hat \beta_2\) 값은 아주 작아지지만 0에 수렴하지 않는다.

ElasticNet

Ridge Regression 과 LASSO 는 각각 장단점이 있다. Ridge 는 상관계수가 높은 변수들의 회귀계수를 정규화 시키고, LASSO 는 특정 회귀계수를 0으로 만들어 변수선택의 효과가 있다. ElasticNet 은 이 두 방법론을 결합함으로써 두개의 장점을 살린다는 특징이 있다. 목적식에 하나만 추가하는 것이 아닌, \(L_1, L_2 \ norm\) 을 동시에 추가한다는 특징이 있다.

\[min\ {1 \over 2} \sum(y_i - \sum \hat\beta_jx_{ij})^2 +\lambda_1 \sum^d_{j=1}\hat\beta^2_j + \lambda_2 \sum^d_{j=1} \mid \hat\beta_j \mid\]

이때 각 penalty 의 hyperparameter 인 \(\lambda\) 는 같은 값이 아니다. 각 \(\lambda\) 값을 조합해 \(\alpha\) 값을 만들 수 있다.

\[\alpha = {\lambda_2 \over \lambda_1 + \lambda_2}\]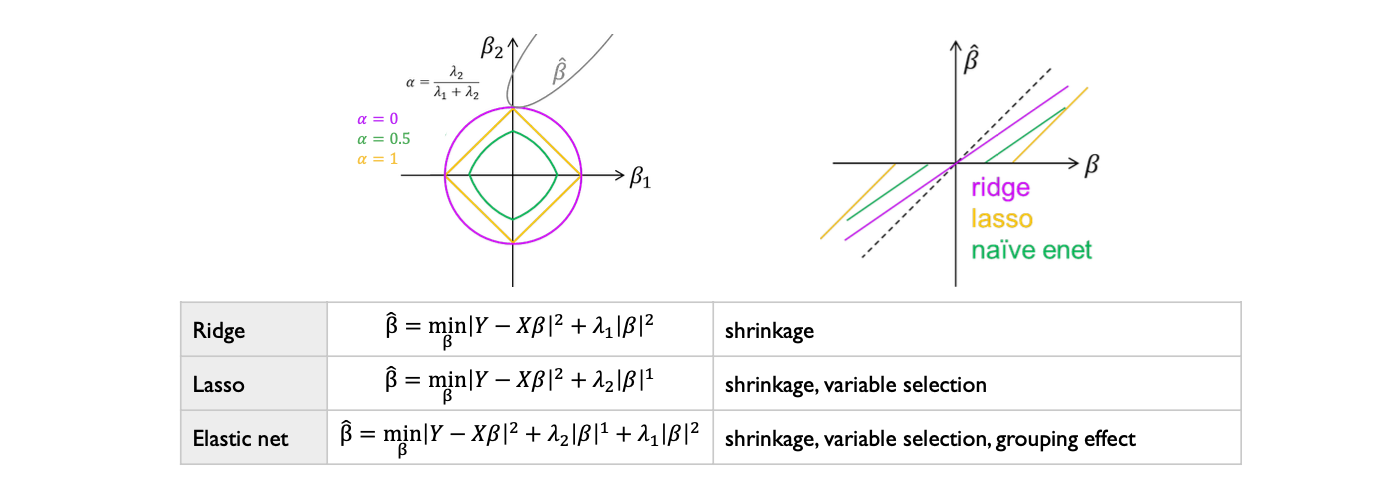

\(\alpha\) 값은 \(\lambda_2\) 의 비율로 해석 할 수 있다. \(\lambda_2\) 값이 \(\lambda_1\) 값보다 비교적 크면 제약식의 영역은 manhattan distance 에 가까워지고, 비교적 적다면 euclidean distance 에 가까워진다.