An Introduction to ROC Analysis (Fawcett, 2006)

Introduction
Classifier Performance
ROC Space
Curves in ROC Space
1. Relative vs. Absolute scores
2. Class skew
3. Creating scoring classifiers
The ROC convex hull
1. The Iso-performance line and Convex hull
2. Operating Conditions
AUROC
Averaging ROC curves
1. Vertical Averaging
2. Threshold Averaging
Multi Class Classification - Class reference formulation
Interpolating classifiers
Conclusion

1. Introduction

Learning from Imbalanced Data (Haibo et. al, 2009) 를 읽다 한가지 재미있는 문단을 발견했다.

In the medical industry, the ramifications of such a consequence can be overwhelmingly costly, more so than classifying a noncancerous patient as cancerous. Therefore, it is evident that for this domain, we require a classifier that will provide high accuracy for the minority class without severely jeopardizing the accuracy of the majority class. Furthermore, this also suggests that the conventional evaluation practice of using singular assessment criteria, such as the overall accuracy or error rate, does not provide adequate information in the case of imbalanced learning. Therefore, more informative assessment metrics, such as the receiver operating characteristics curves, precision-recall curves, and cost curves, are necessary for conclusive evaluations of performance in the presence of imbalanced data. (Haibo et al, 2009)

ROC 에 대한 전반적인 개념은 알고 있지만, confusion matrix 와 여러가지 평가지표들을 마주할 때 마다 압도되어 개념을 항상 다시 찾아봐야 하는 상황이 종종 일어난다.

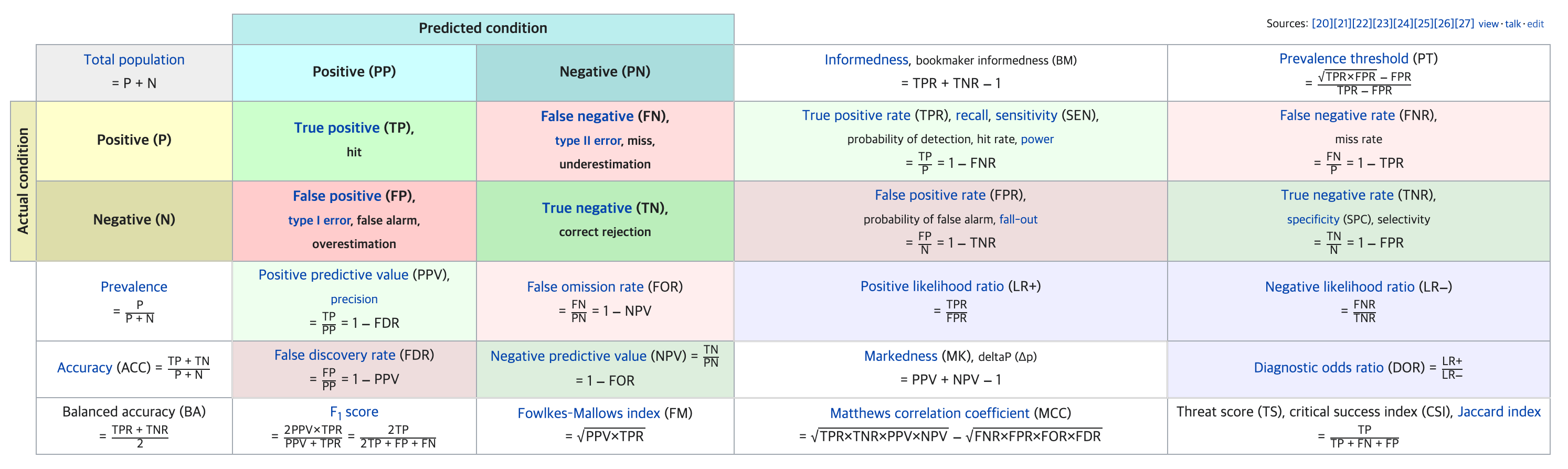
헷갈릴법도 하다.

읽고 있던 논문에서 콕 집어 imbalanced data 에선 ROC 가 좋은 성능평가지표라고 언급을 했기 때문에 ROC 관련 유명한 논문인 An introduction to ROC analysis, Fawcett, 2006 을 리뷰해보고자 한다. ROC 만큼 머신러닝의 근본이 되는 평가지표를 완전히 자신만의 것으로 만드는 데 손해볼 건 없기 때문이다.

Reciever Operation Characteristics graph (ROC graph) 는 분류기를 시각화하고, 정리하고, 선택하는데 유용한 도구다. Signal detection theory 에 기반을 두고 있으며, 머신러닝에서 본격적으로 사용되기 전에는 의학계와 diagnostic systems 에서 많이 사용되었다. Learning from Imbalanced data 에서도 언급이 된 것 처럼, 일반적인 classification accuracy 는 분류기의 성능을 평가하는데 좋은 지표가 아니다. ROC 는 분류기의 성능평가지표로 준수한 성능을 보이고, 추가적으로 skewed class distribution (imbalanced data) 와 균일하지 않은 classification error cost 도메인에서도 좋은 성능을 보여준다.

ROC 의 기본 개념은 간단하지만, 단면적으로는 나타나지 않는 복잡함이 숨겨져 있다. 그렇기 때문에 ROC 가 정확히 어떤 원리로 작동하며, 기본적인 ROC 도출을 넘어 실제 상황에서 어떤 식으로 응용되는지 알 필요가 있다.

2. Classifier Performance

아주 간단한 분류기를 예시로 들어보자. 하나의 샘플은 실제 값 Positive, Negative가 존재하며, 분류기는 학습에 따라 해당 샘플을 Positive 혹은 Negative 로 분류 할 것이다. 그렇기 때문에 하나의 샘플에겐 4개의 경우의 수가 있다.

Positive 라고 분류했는데 실제로 Positive 인 경우: True Positive

Negative 라고 분류했는데 실제로 Positive 인 경우: False Negative

Negative 라고 분류했는데 실제로 Negative 인 경우: True Negative

Positive 라고 분류했는데 실제로 Negative 인 경우: False Positive

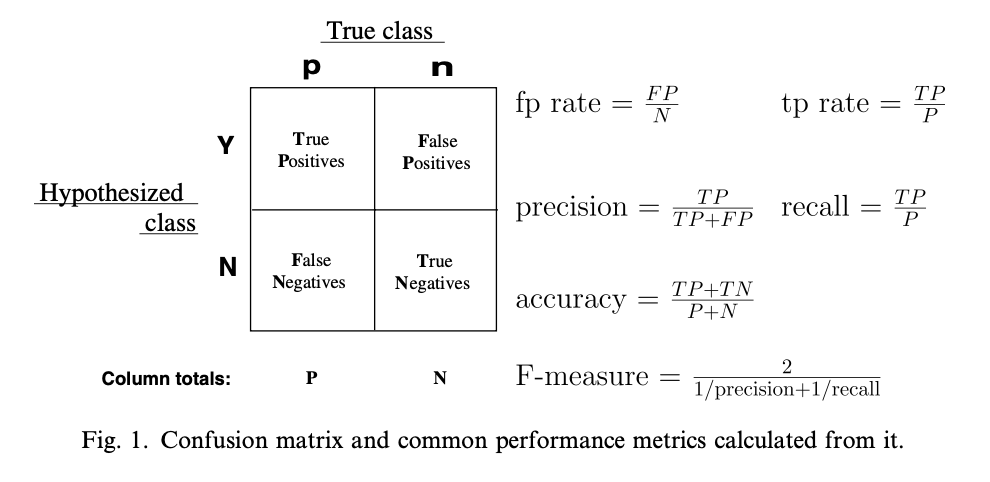
이 경우들을 모아 위와 같은 confusion matrix 를 만들 수 있다. 그리고 이 confustion matrix 를 통해 TP rate 와 FP rate 를 계산 할 수 있다. TPR 은 실제로 Positive 한 샘플들 중 Postive 하다고 맞춘 비율 을 나타내며, FPR 은 실제로 Negative 한 샘플들 중 Positive 하다고 맞춘 비율 을 나타낸다.

그리고 ROC 에서 사용하는 용어들은 다른 domain 에선 다른 이름을 갖는데, 별명이라고 생각하면 된다.

TPR = Sensitivity = Recall = Hit Rate

Specificity = 1 - FPR

Positive predictive value = Precision

TPR 과 FPR 을 계산하는 방법을 보면 쉽게 알 수 있는데, 분류기의 성능이 좋을수록 TPR 은 높고 FPR 은 낮다.

3. ROC Space

ROC 그래프에는 x 축에 해당 분류기의 TPR을, y 축에 해당 분류기의 FPR 을 표시한다. 해당 분류기의 benefit (True Positives) 와 costs (False Positives) 를 시각적으로 표현한 것이다.

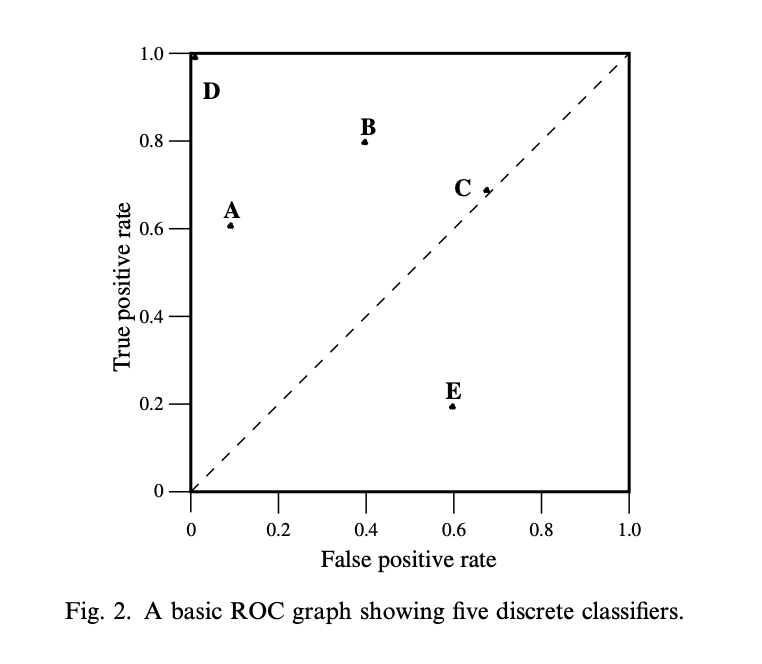
위 예시는 5개의 discrete classifier 을 ROC 그래프에 표시한 것이다. D 분류기의 TPR 은 1이고 FPR 은 0이므로 완벽한 분류 성능을 가졌다고 볼 수 있다. 전반적으로 ROC 그래프의 좌측 상단에 분류기가 위치해 있다면 더 좋은 성능을 보인다고 해석 할 수 있다. 또한, 분류기가 비교적 좌측에 위치해 있다면 해당 분류기가 ‘conservative’ 하다고 한다. 이는 FPR 이 낮기 때문인데, ‘쉽게’ 어떤 샘플을 positive 하다고 분류하지 않는다는 것을 의미한다. 반대로 분류기가 비교적 우측에 위치해 있다면 해당 분류기가 ‘liberal’ 하다고 한다. 이는 해당 분류기가 비교적 ‘쉽게’ 어떤 샘플을 positive 하다고 분류한다는 것을 의미한다. 위 그림을 예시로 들면 A 는 B 보다 상대적으로 ‘conservative’ 하다고 볼 수 있다.

ROC 그래프엔 대각선의 점선 (\(y=x\)) 이 있는데, 이는 random performance line 이다. 대각선 위에 위치해 있는 분류기는 어떤 샘플을 분류 할 때 랜덤하게 클래스를 맞추는것과 다름없는 성능을 보인다는 뜻이다. 어떤 분류기가 랜덤으로 샘플이 Positive 하다고 맞춘다면, 반은 맞고 반은 틀릴 것이다. 그렇게 되면 TPR = FPR = 0.5 이고, 해당 분류기는 random performance line 위에 놓이게 된다.

다른 분류기를 예시로 들어보자. 이 분류기는 90% 확률로 어떤 샘플이 Positive 하다고 맞춘다. 이 분류기의 TPR은 0.9 이지만, 똑같이 FPR 도 0.9 일 것이다. 그렇기 때문에 분류기는 random performance line 위에 놓이기 위해 학습이 되어야 한다는 것을 의미한다. 반대로 생각하면, random performance line 아래에 위치한 분류기는 랜덤하게 맞추는 것보다 못한 성능을 보인다는 뜻이므로 대부분의 ROC 그래프에선 표시조차 안한다.

4. Curves in ROC Space

Decision Tree 같은 분류기들은 대부분 이산형/binary 값을 예측한다. 이와 같은 이산형 분류기를 test set 에 대입하면 하나의 confusion matrix 가 도식된다. 이는 지금까지 봐왔던 예시처럼 ROC Space 에 하나의 점으로 표시된다는 뜻이다.

하지만 인공신경망이나 Naive Bayes 분류기 같은 경우는 하나의 샘플에 대한 확률/점수를 뱉는다 (편의상 이런 분류기를 연속형 분류기라고 부르겠다. 원래는 probabilistic classifier 가 옳은 terminology 다). 이 확률/점수는 해당 샘플이 특정 클래스에 속해있을 정도를 나타낸다. 이런 연속형 분류기에 threshold 를 도입하면 이산형 분류기와 같은 효과를 볼 수 있다. 더 정확히는 threshold 를 설정함에 따라 샘플의 output 이 달라진다.

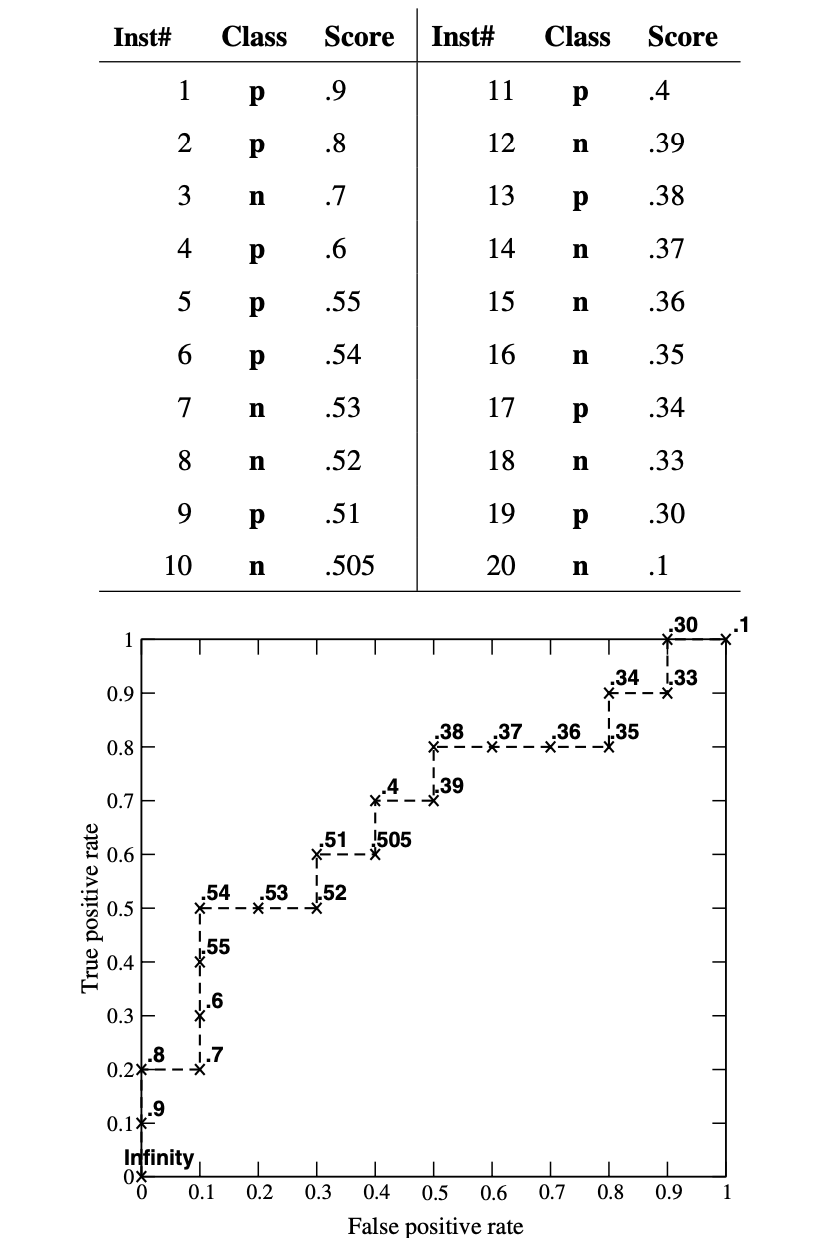
위 예시는 Naive Bayes 분류기에서 threshold 를 조정함에 따라 성능을 ROC 그래프에 도식한 것이다. 각 점 위에 있는 소숫점 수가 해당 분류기의 threshold 이다. 계산 예시를 통해 이해를 해보자면, 먼저 첫 threshold 를 0.9로 잡은 분류기의 TPR과 FPR 을 계산해 보자. 표를 참고하면 threshold 인 0.9보다 크거나 같은 샘플은 하나 (instance 1) 뿐이므로,

\[TPR = {tp \over p} = {1 \over 10}=0.1 \\ FPR = {fp \over n} = {0 \over 10}=0\]

인 분류기가 ROC 그래프에 찍히는 것이다. Threshold 를 조정하며 위와 같은 과정을 반복하면 최종적인 ROC curve 를 완성 할 수 있다. 참고로 위 예시에서 Accuracy 가 가장 높은 모델은 threshold 가 0.54 일 때다.

\[Accuracy = {tp+tn \over p+n} = {5+9 \over 20} = 0.7 = 70 \%\]

이처럼 ROC 를 통한 분류기의 정량적 성능평가가 가능하다. 추가적으로 ROC 는 몇가지의 장점을 가지고 있다.

4.1 Relative vs. Absolute scores

ROC 의 첫번째 장점은 좋은 상대적인 인스턴스 점수를 낸다는 것이다.

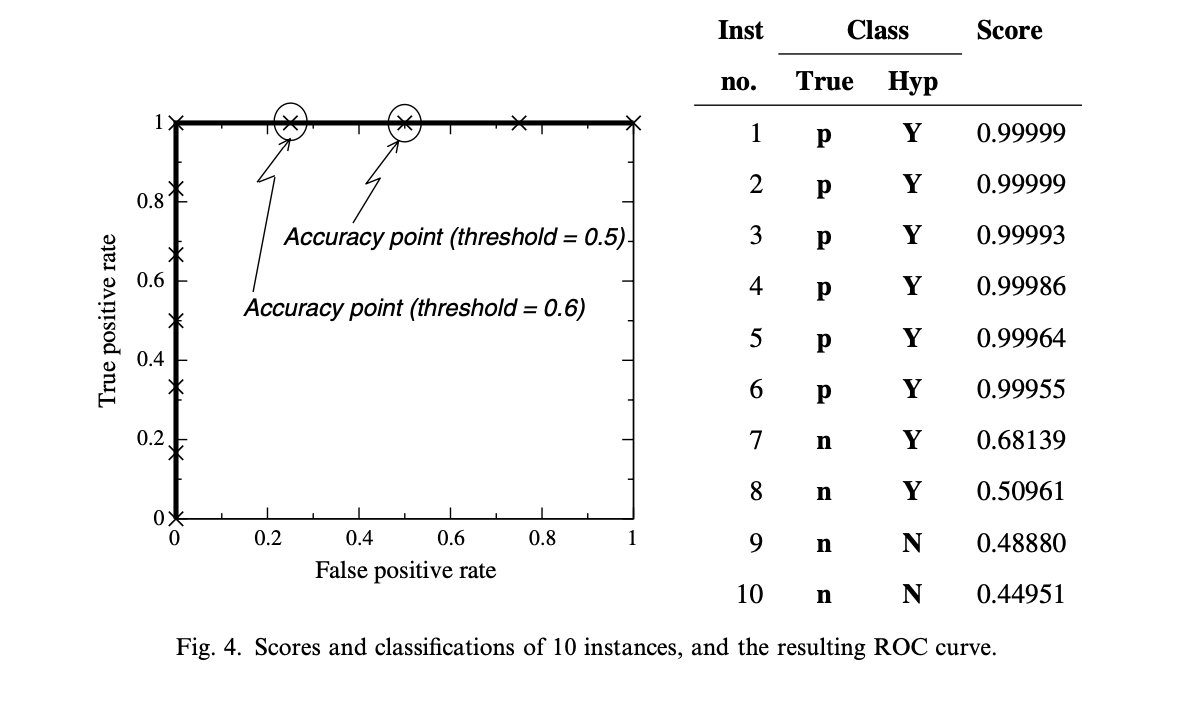
위 그림은 Naive Bayes 분류기에서 도출한 인스턴스 점수와 ROC 그래프다. Threshold 는 0.5로 설정한 것을 알 수 있다. 이 경우엔 인스턴스 7,8 이 잘못된 분류를 하여 Accuracy 가 80% 인 것을 알 수 있다. 하지만 같은 분류기를 ROC 그래프에 도식화하면 완벽한 분류기의 모습을 보인다. 이는 근본적으로 ROC 가 모델을 평가하는 방법론이 다르기 때문이다.

ROC 가 평가하는 성능은 FPR 대비 TPR 이고 (relative), Accuracy 는 절대적 성능평가지표다 (absolute). Threshold 가 0.5인 경우를 예시로 들어보자.

\[TPR = {tp \over p} = {6 \over 6} = 1\\ FPR = {fp \over n} = {2 \over 4}=0.5\\ Accuracy = {tp+tn \over p+n} = {8 \over 10} = 0.8 = 80 \%\]

Threshold 를 각 인스턴스의 점수로 정하고 위와 같은 계산을 반복해도 모든 인스턴스의 TPR 은 1이 나오므로, 예시의 그림과 같은 ROC 그래프가 그려진다. 반면 Threshold 를 조정하며 Accuracy 를 계산해 보면 결과가 매번 다르다. 그렇기 때문에 ROC는 relative score 을 도출하는데 있어 Accuracy 보다 훨씬 좋은 성능지표로 사용 할 수 있다.

4.2 Class skew

ROC 의 두번째 장점은 클래스 변화에 robust 하다는 점이다. 이는 Learning from Imbalanced Data (Haibo et. al, 2009) 에서 직접적으로 언급한 부분으로써, 현실 데이터는 클래스 쏠림현상이 어느정도 있다는 점을 고려해보면 ROC의 가장 큰 장점 중 하나이다. 만약 데이터셋에서 Positive/Negative 인스턴스의 비율이 변해도 ROC는 변하지 않는다. 이는 Relative strength 와 같은 맥락에서 왜 그런지 해석 할 수 있다. 만약 데이터셋의 클래스 비율이 변하면 분류기가 뱉는 Confusion matrix 의 값도 변하는데, confusion matrix 의 양 column 을 사용하는 성능평가지표는 이에 따라 변하지만 ROC 는 변하지 않는다. 다시 한번 복기해보자면 ROC 는 TPR, FPR 만 사용하기 때문이다.

이는 특히 시계열 데이터를 분석하는데 유용한 특성이 된다. 코로나19 의 확진자에 대한 abstract 데이터셋을 사용한다고 가정해보자. 팬데믹 국면은 매일같이 변하므로, 이에 따라 특정 분류기가 구축하는 confusion matrix 또한 변할 것이다. 이때 ROC 를 성능평가지표로 사용하게 된다면 업데이트 되는 데이터셋에 따라 변하지 않는다는 장점이 있다.

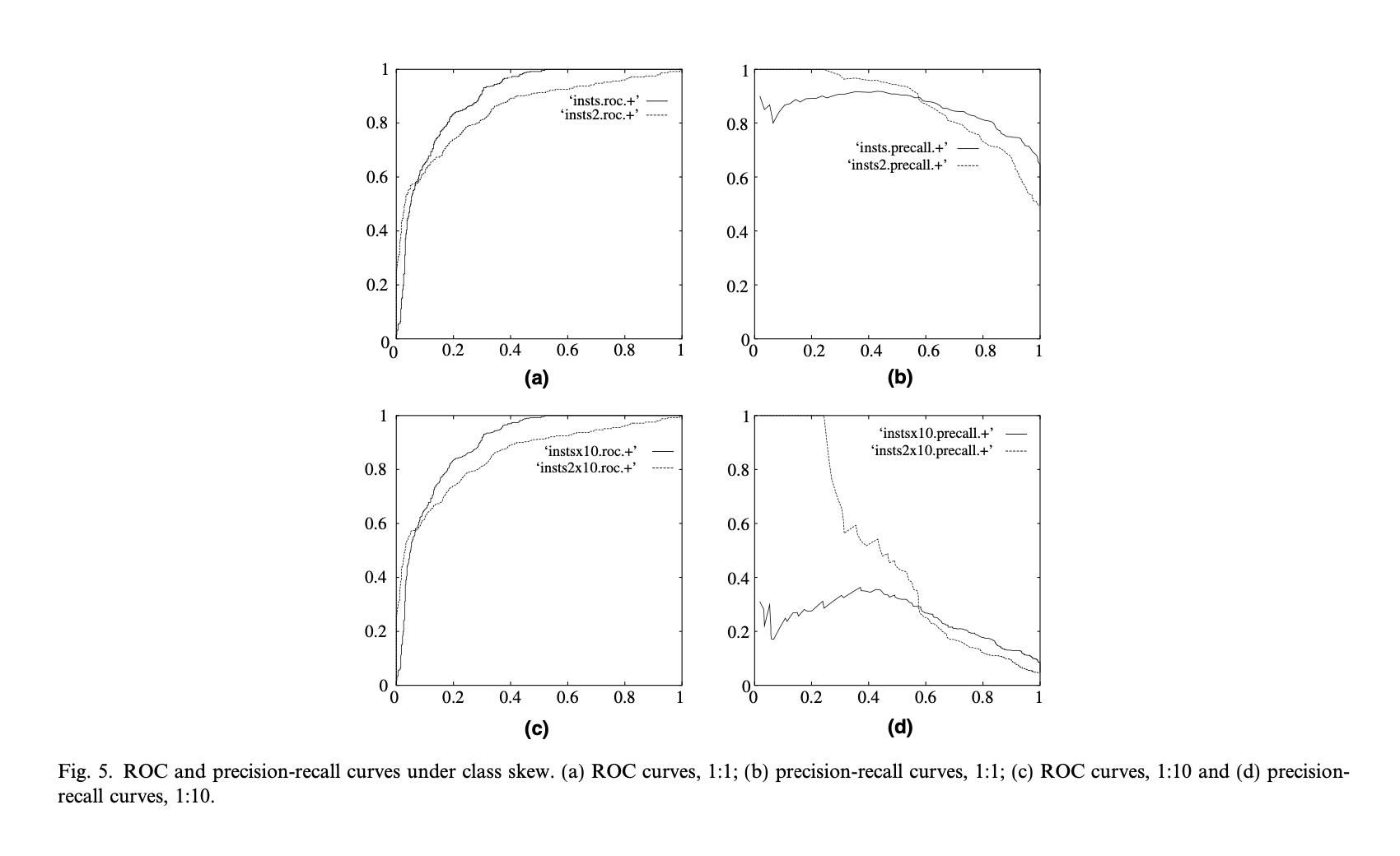
위 예시를 확인해 보자. a, b 는 각각 1:1 클래스 비율을 가진 ROC 와 Precision-Recall 그래프다. c, d 는 해당 모델의 데이터셋의 Negative 클래스를 10배 늘린 뒤 다시 그린 ROC 와 Precision-Recall 그래프다. 클래스의 분포만 바뀌었을 뿐, 데이터의 본질적인 concept는 변하지 않았다. ROC 그래프는 형상을 유지하는 반면, Precision-Recall 그래프는 완전히 다른 형상을 띈다.

4.3 Creating scoring classifiers

많은 분류기 모델은 discrete 하다. 이는 분류기가 인스턴스당 출력하는 output 이 binary 하단 것을 의미하고, 이런 이산형 분류기는 ROC 그래프 상 하나의 점으로만 표현 할 수밖에 없다. 하지만 이런 이산형 분류기로도 ROC curve 를 그리는 방법이 존재한다. 분류기가 클라스 라벨 대신 probabilisitc classifier 처럼 클라스 점수를 생성하게 하면 된다. 해당 논문엔 이 방법론에 대해 깊게 들어가지 않지만, Provost and Domingos, 2001 같은 참고문헌을 제시한다.

Decision tree 를 짧은 예시로 들어보자. Decision tree 는 하나의 노드에서 가장 우세한 클라스를 통해 분류를 진행한다. 해당 노드에서 존재하는 클라스의 비율을 점수로 사용하는 방법을 Provost and Domingos, 2001 에서 제시한다.

5. The ROC convex hull

5.1 The Iso-performance line and Convex hull

지금까지 probabilistic classifier 의 ROC curve 에 대한 특성들을 살펴보았다. 이쯤되면 ROC curve 위의 어떤 threshold point 가 최적일까 라는 의문이 들 수 밖에 없다. 이를 알기 위해 convex hull 이란 개념을 알고 가야한다.

Convex hull 을 알기 위해 먼저 iso-performance line 을 알아야 한다. Iso-performance line 이란 동일한 성능, 혹은 동일한 cost 를 갖는 threshold 의 선이다. Random performance line 위의 모든 분류기가 같은 성능을 갖는 것과 동일한 개념이다. 그리고 해당 선은 두 ROC point 의 기울기로 구할 수 있다.

\[{TP_2-TP_1 \over FP_2-FP_1} = {c(Y,n)p(n) \over c(N,p)p(p)} = m\]

ROC space 위 두 점 \((FP_1, TP_1), \ (FP_2, TP_2)\) 가 존재한다고 생각해보자. 두 점을 선으로 잇고 이 선의 기울기는 위의 식으로 구할 수 있는데, 해당 선의 기울기 \(m\) 이 바로 Iso-performance line 의 기울기다. 기울기 \(m\) 을 가진 Iso-performance line 위의 모든 분류기는 같은 성능을 보인다.

이 개념을 가지고 ROC curve 내의 모든 threshold point 를 가지고 Iso-performance line 을 구축 한 뒤, 좌측 상단쪽에 근접한 선들만 남기면 ROC convex hull 을 그릴 수 있다. 만약 하나의 ROC curve 가 아닌, 다중의 분류기를 ROC 그래프 선상에 표시하게 되더라도 같은 원리로 ROC convex hull 을 구축한다.

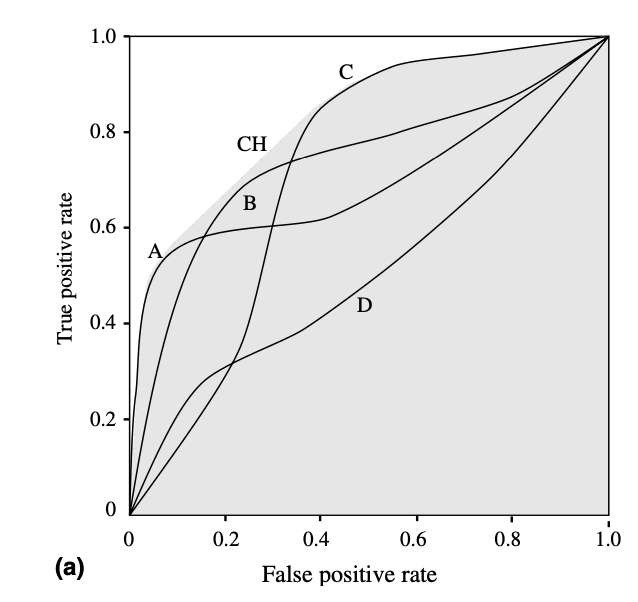
위 예시를 보자. 서로 다른 분류기 A,B,C,D 가 있고, 해당 분류기들로부터 구한 가장 좌측 상단의 iso-performance line 들을 남겨 만든 ROC convex hull 은 CH 로 표시되어 있다. 일단 4개의 분류기를 비교하는 경우에선 분류기 B, D 는 convex hull 과 맞닿아 있지 않으므로 최적의 분류기에서 완전히 제외시킬 수 있다. 추가적으로 A, C 분류기의 threshold point 들 중 convex hull 과 맞닿아 있지 않는 점들 또한 최적의 분류기에서 제외할 수 있다.

5.2 Operating Conditions

위에서 언급하였듯이 ROC 의 최대 장점 중 하나는 class distribution (or class skew) 과 error cost 에 대한 robustness 이다. 해당 데이터셋의 operating conditions (class skew, error cost) 의 변화에도 그래프 자체는 변하지 않는다. 변하는 것은 최적의 분류기를 구분하는 방법이다. Operating conditions 가 ROC를 처음 구한 시점에서 달라졌다면 최적의 분류기는 어떻게 구할까?

\[TPR = {neg \over pos} \cdot FPR + {acc-neg \over pos}\]

위 공식은 Iso-performance line 의 또다른 표기법이다. Line 의 기울기는 해당 모델/데이터셋의 Positive 과 Negative 간의 비율이며, operating conditions 의 변화에 따라 최적의 분류기 threshold point 도 변한다.

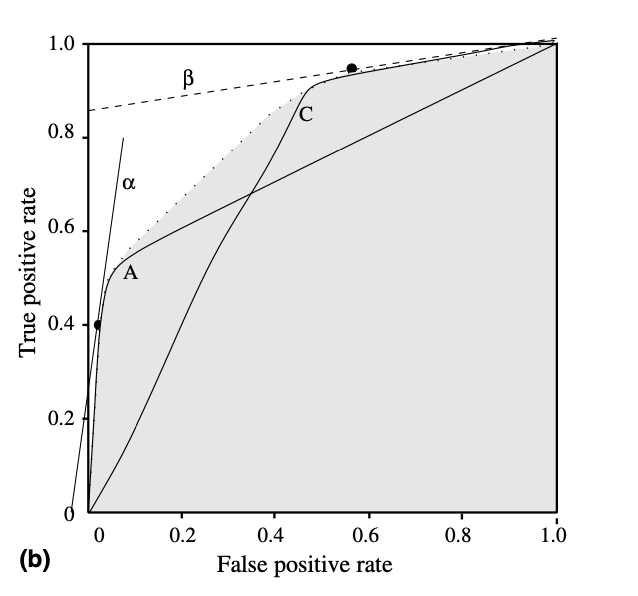
위 예시를 보자. 두개의 분류기 A,C 가 있다. 만약 시간이 지나며 새로운 데이터 샘플들이 축적되고, operating conditions 가 변했다고 가정하자. 이 경우에선 negative 인스턴스가 positive 인스턴스보다 10배 더 많아졌다. 그렇다면 위의 식에 따라 기울기는 \(m=10\) 으로 변하고, 기울기가 10인 convex hull 위의 Iso-performance line 은 \(\alpha\) 다. 이 경우에선 \(\alpha\) 와 분류기 A 가 만나는 지점이 바로 분류기 A,C 통틀어 최적의 분류기인 셈이다.

만약 Operating conditions 가 변했는데 최적의 Iso-performance line 과 맞닿아 있는 ROC curve 가 없으면, 9장에서 설명할 Interpolating classifier method 를 사용하면 된다.

6. AUROC

지금까지 단일 분류기의 성능평가에 대해서 중점적으로 다루었다. 하지만 ROC는 성능평가지표이므로, 궁극적으로 2개 이상의 분류기의 성능을 비교하기 위해 사용한다. 그러기 위해서 비교하고 싶은 두 모델에 대해 ROC curve 를 비교하면 될거라 생각 할 수 있지만, 현실은 조금 더 복잡하다. 두개의 분류기를 ROC 그래프에 모델링 하더라도 어떤 분류기의 성능이 더 좋은지 바로 눈에 띄는 경우는 드물다. 그렇기 때문에 \(n\) 개의 분류기를 하나의 scalar value 로 비교 할 수 있게 하는 AUROC 를 계산한다.

AUROC (Area Under ROC Curve) 는 말 그대로 ROC curve 아래의 면적이다. x 축과 y 축의 범위는 둘다 0~1 이기 때문에 \(0 \leq AUROC \leq 1\) 가 성립한다. 하지만 앞서 언급했듯이 ROC curve 가 random performance line 아래에 있다면 해당 분류기는 기각해도 되기 때문에, 실질적인 AUROC 의 범위는 \(0.5 \leq AUROC \leq 1\) 가 된다.

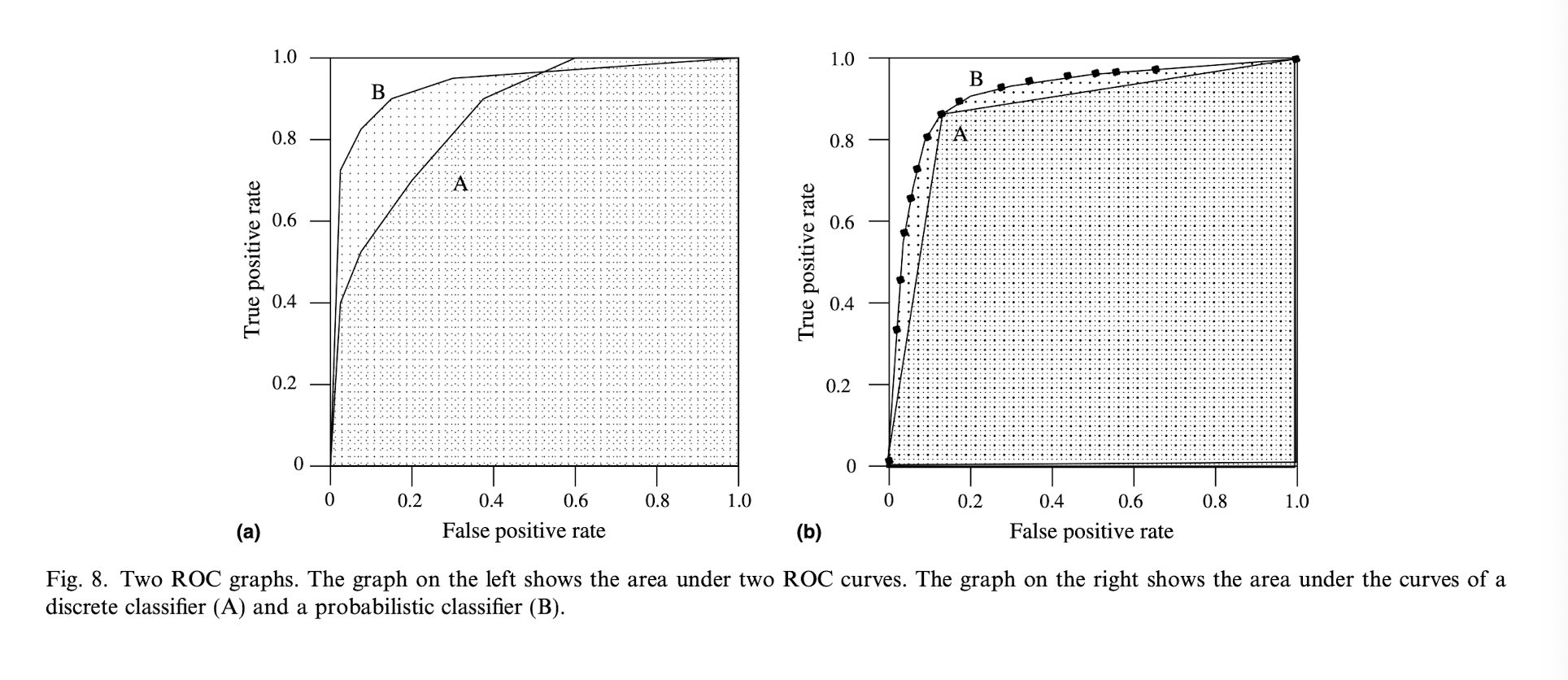
좌측의 그래프는 두개의 분류기 A, B 의 AUROC 다. 분류기 B 의 AUROC 가 A 보다 크기 때문에 하나의 scalar value 로 우리는 분류기 B 의 성능이 더 좋다고 평가할 수 있다. 이때 \(FPR \geq 0.6\) 의 범위를 주목해보자. 이 범위 이상으론 실질적으로 A의 성능이 B 보다 뛰어나다. 하지만 현실에선 이정도의 discrepancy 정도는 AUROC 의 단일값이 더 큰 indicator 로 작용한다.

우측의 그래프는 binary classifier A 와 probabilistic classifier B 의 AUROC 다. A의 threshold 에서 A와 B 의 성능은 동일하지만, 전반적으로 B 의 AUROC 가 더 넓기 때문에 B의 성능이 더 좋다는 것을 알 수 있다.

7. Averaging ROC curves

지금까지 Iso-performance line 과 convex hull 을 통해 단일 분류기의 최적의 threshold 를 구하는 과정과, AUROC 를 통해 \(n\) 개의 분류기의 성능비교를 하는 과정을 서술했다. 지금까지의 전제는 test set 을 한번에 사용해서 분류기의 ROC curve 를 그렸지만, 분류기를 학습시키고 test 를 진행 할 때 test set 을 통째로 쓰는 경우는 드물다. 현실에선 cross-validation 이나 bootstrap method 를 통해 test set \(T_M\) 을 \(T_1, T_2,...,T_n\) 으로 쪼개 분류기를 test 하며, 각 test set 에선 각자의 ROC curve 가 생성된다.

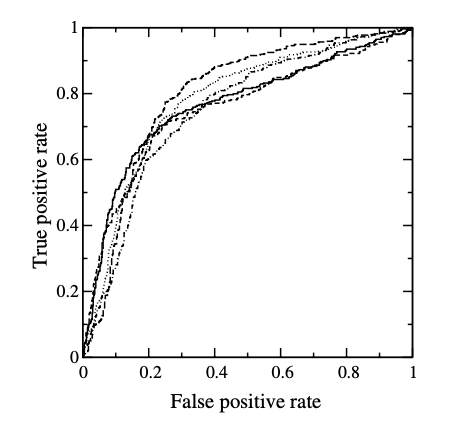
위 그림은 test set 을 5개로 나눈 분류기의 ROC curve 이다. 그렇다면 이 단일 분류기에서 나온 5개의 ROC curve 중 어떤 curve 를 사용해야 할까? 단순하게 생각해보면 성능이 제일 높은 (AUROC 가 제일 큰) curve 를 해당 분류기의 성능이라고 생각 할 수 있지만, 이는 하나의 test set 에서 나온 성능평가지표들 중 최댓값의 set 을 분류기의 성능이라고 말하는 것과 동일하다. 분산에 대한 정보가 사라지므로 이 방법은 기각된다. 애초에 test set 을 sampling 한 이유가 실험에 대한 통계적인 정보를 포함시키기 위한 것이기 때문에, \(n\)개의 test set 으로부터 나온 ROC curve 들의 averaging 을 진행해야 한다.

7.1 Vertical Averaging

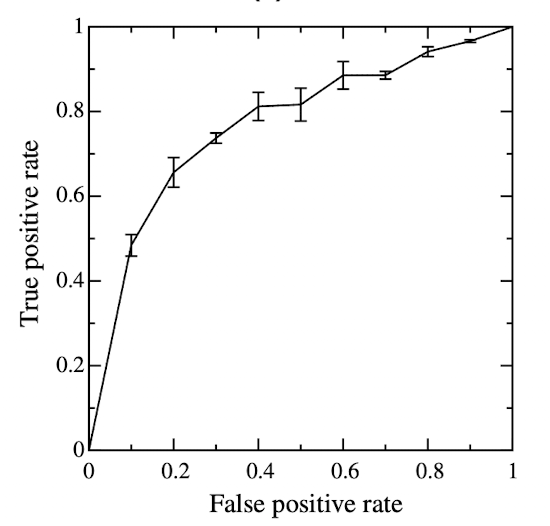
Vertical Averaging 은 ROC curve averaging 의 첫 방법론이다. Vertical averaging 에선 각 ROC curve 를 함수로 생각하고, FPR 이 독립변수, TPR 이 종속변수가 된다. 즉 \(TPR = R_i(FPR)\). Average ROC curve 는 \(\hat{R}(FPR)=mean[R_i(FPR)]\) 를 통해 그려진다. 이때 각 구간의 신뢰도는 이항분포를 따른다.

위 예시는 5개의 ROC curve 의 vertical average 이다. Vertical bar 은 ROC mean 에서 95% 신뢰구간을 나타내고, 위 예시에서는 FPR 을 0.1 구간으로 총 10번 샘플링 한 것이다. 물론 더 촘촘하게 샘플링을 할 수도 있지만, ROC의 주 목적은 시각화이기 때문에 적당한 구간을 정하는게 좋다.

7.2 Threshold Averaging

Vertical averaging 은 종속변수 TPR 하나로 Average ROC curve 를 계산할 수 있다는 장점을 가지고 있다. 하지만 이 TPR 은 독립변수인 FPR 에서 계산된 것인데, 대부분의 경우에서 FPR 은 연구자가 직접적으로 control 할 수 없다는 단점 또한 있다. 연구자가 직접 control 할 수 있는 threshold 나 classifier 점수를 독립변수로 정해 Average ROC curve 를 구할 수 있는 방법론이 바로 Threshold Averaging 이다.

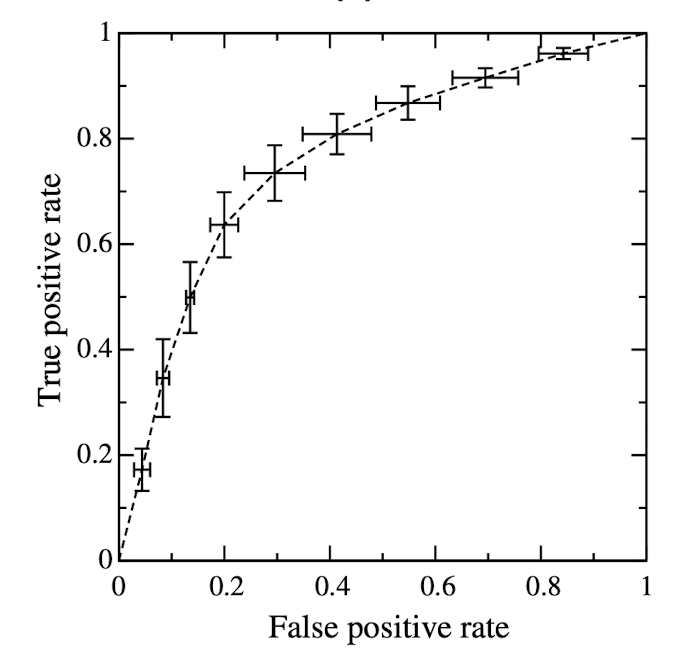
FPR을 기준으로 구간을 나누어 sampling 하는 vertical averaging 와는 다르게, threshold averaging 은 말 그대로 threshold 를 정해서 해당 점에서 averaging 을 진행하는 것이다. 이때 간단한 알고리즘을 통해 sampling 할 threshold 를 정할 수 있다. 위 그림은 threshold sampling 알고리즘을 통해 추출된 threshold 를 독립변수로 지정한 threshold average 이다. 이때 vertical averaging 처럼 x 축인 FPR 을 독립변수로 사용하지 않았기 때문에 TPR 과 FPR 에 대한 신뢰구간을 동시에 보여준다는 장점이 있다.

8. Multi Class Classification - Class reference formulation

대부분의 ROC 에 대한 연구가 그렇듯이, 지금까지의 전제는 이진 분류기였다. 애초에 ROC 가 가장 많이 사용되는 분야는 의학계이므로, multi class classification 을 굳이 염두에 둘 필요가 없었다. 이진 분류를 통해 직관적으로 cost (false positives) 와 benefit (true positive) 의 tradeoff 를 이해할 수 있다. 하지만 성능평가를 하고싶은 분류기가 다중 분류기라면 ROC의 개념들을 적용하는건 전혀 직관적이지가 않다.

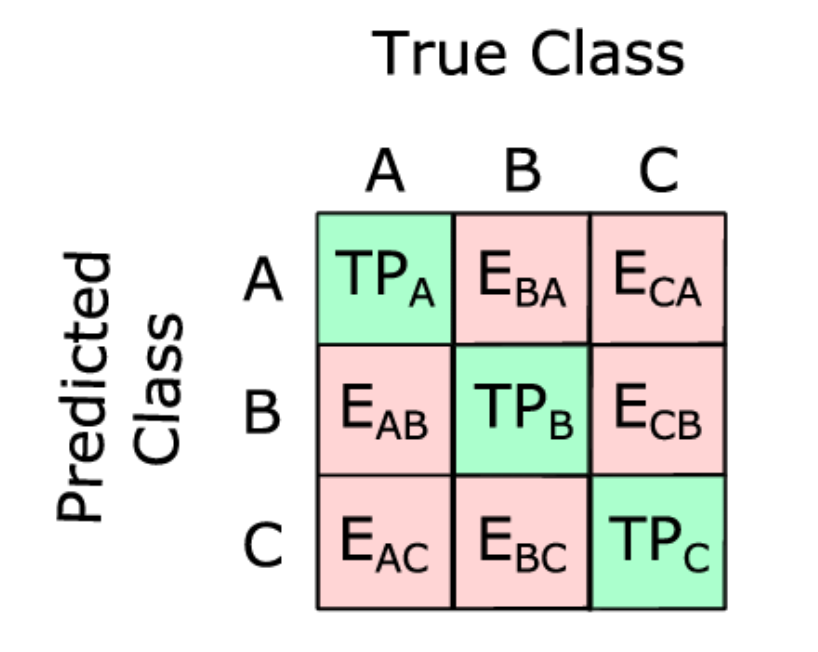
\(n\)개의 클래스를 갖는 문제는 \(n \times n\) confusion matrix 를 만들고, 대각선 성분인 \(n\)개의 정답과 나머지 성분인 \(n^2 - n\) 개의 오답으로 구성되어 있다. 즉 TP 와 FP 간의 tradeoff 대신 \(n\)개의 benefit 과 \(n^2 - n\) 개의 cost 간의 tradeoff 를 염두에 둬야 한다. 이때 우리가 익숙한 2차원의 ROC space 는 \(n^2 - n\) 차원의 정다포체가 된다. 이런 경우에서 ROC analysis 를 진행하는 방법 중 하나는 class reference formulation 이다.

Class reference formulation 은 \(n\)개의 클래스를 위해 \(n\)개의 ROC 그래프를 생성하는 방법이다.

\[P_i = c_i \\ N_i = \bigcup_{j \neq i} c_j \in C\]

\(C\) 가 모든 클래스를 포함한 집합이고 \(c_i\) 가 \(C\) 의 원소들이면, 모든 \(i\) 를 위해 \(c_i\) 를 positive class 로 두고 나머지 클래스들을 negative class 로 둔 뒤 ROC curve 를 생성하는 원리다.

9. Interpolating classifiers

ROC convex hull 을 통해 최적의 성능을 내는 구간을 표시할 수 있다는 것을 앞서 설명했다. 하지만 만약 원하는 성능을 생성한 분류기를 통해 얻지 못한다면, 기존의 분류기들의 결정을 샘플링 하여 원하는 성능의 분류기를 구축 할 수 있다.

CoIL Challenge 2000 (van der Putten and Someren, 2000) 에서 나온 분류 문제를 예시로 들어보자. 이 문제엔 보험사와 4,000 명의 고객이 존재한다. 보험사의 예산은 약 800명의 고객에게 상품소개를 할 정도이고, 상품소개를 받은 고객 중 보험을 살 고객의 기댓값은 6%다. 기댓값을 계산해보면 4,000명의 고객 중 240명은 보험을 구매할 것이고 (positive), 3760명은 보험을 거절할 것이다 (negative). 보험사의 목표는 4,000명의 고객 중 보험을 구매할 확률이 가장 높은 800명에게 상품소개를 하는 것이다.

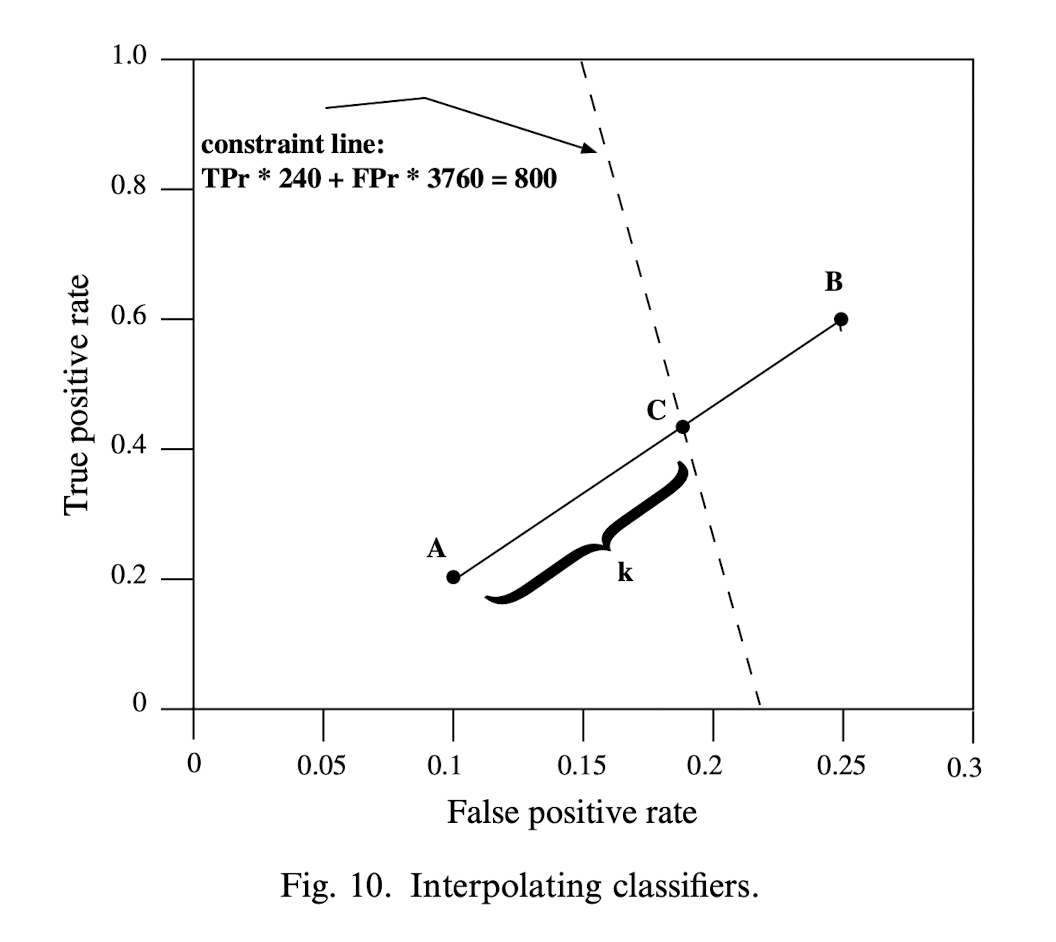
고객이 보험을 구매할 확률을 점수화 하는 두개의 분류기 A, B 를 생성했다고 가정하자. A 는 (0.1, 0.2) 에 위치해 있고, B 는 (0.25, 0.6) 에 위치해 있다. 800명에게만 상품소개를 할 수 있다는 제약이 있으므로 새로운 제약식 \(FPR \times 3706 \ + \ TPR \times 240 = 800\) 을 정의할 수 있다. 이 제약식을 통해 구한 A의 기댓값은 424명이고 B 의 기댓값은 1084다. 그러므로 A와 B 사이 있는 적절한 분류기를 찾는 것이 목표가 된다.

ROC space 에 해당 제약식을 표시한 뒤 A 와 B 를 연결하면 두 선의 접점에 C 라는 점이 생긴다. C 의 TPR, FPR 을 갖는 분류기는 이때 최적의 성능을 보일 것이다. 이 새로운 분류기 C 는 A와 B를 적절히 샘플링 하면 된다. 이 샘플 비율은 C의 비례 거리를 통해 계산 할 수 있다.

\[k = {0.18 - 0.1 \over 0.25 - 0.1} \approx 0.53\]

B의 예측치들을 0.53의 비율과 A의 예측치들을 0.47의 비율로 샘플링 한다면 분류기 C 의 성능을 갖는 분류기를 생성할 수 있다.

10. Conclusion

ROC는 분류기를 분석하고 시각화하는데 있어 아주 효과적인 성능평가 방법론이다. Accuracy, error rate, error cost 같은 단일값의 성능평가지표보다 훨씬 뛰어난 insight 를 제공하며, class imbalance 와 변하는 operating conditions 에 robust 하다는 강점이 있다.

Contents