The Perceptron and Gradient Descent
Contents
- Introduction
- The Perceptron
- Gradient Descent
- Taylor Expansion and the Chain Rule
- Stochastic, Batch, and Minibatch Gradient Descent
해당 포스트는 2021년 1학기 고려대학교 강필성 교수님의 ‘다변량분석’ 강의를 참고하여 작성되었습니다.
이미지는 강필성 교수님의 강의 슬라이드에서 발췌하였습니다.
A+ 감사했습니다 교수님
Introduction
Biomimicry
Biomimicry 란 자연에서 볼 수 있는 디자인적 요소들이나 생물체의 특성들을 연구 및 모방하는 분야다. 딥러닝의 초기 모델인 인공신경망은 사람의 뇌의 Biomimicry 모델이며, 최적화 이론에선 유전 알고리즘, Ant Colony Algorithm, Particle Swarm Optimization 등이 대표적인 Biomimicry 방법론들이다.
The world is poorly designed. But copying nature helps. Vox 에서 만든 Biomimicry 에 대한 영상이다. 굉장히 흥미롭다.
생물시간에 우리의 뇌는 뉴런들끼리 서로 전기신호를 통해 정보를 전달한다고 배운다. 퍼셉트론은 이런 정보를 전달하는 가장 기초 단위인 뉴런을 흉내낸 지도학습 알고리즘이다. 처음엔 단일 분류기 모델로 고안되었지만, 수십년 후 딥러닝이란 학문의 시초가 되었다. 가장 복잡한 딥러닝 모델의 building block 도 결국 퍼셉트론에서 시작되기 때문이다.
The Perceptron
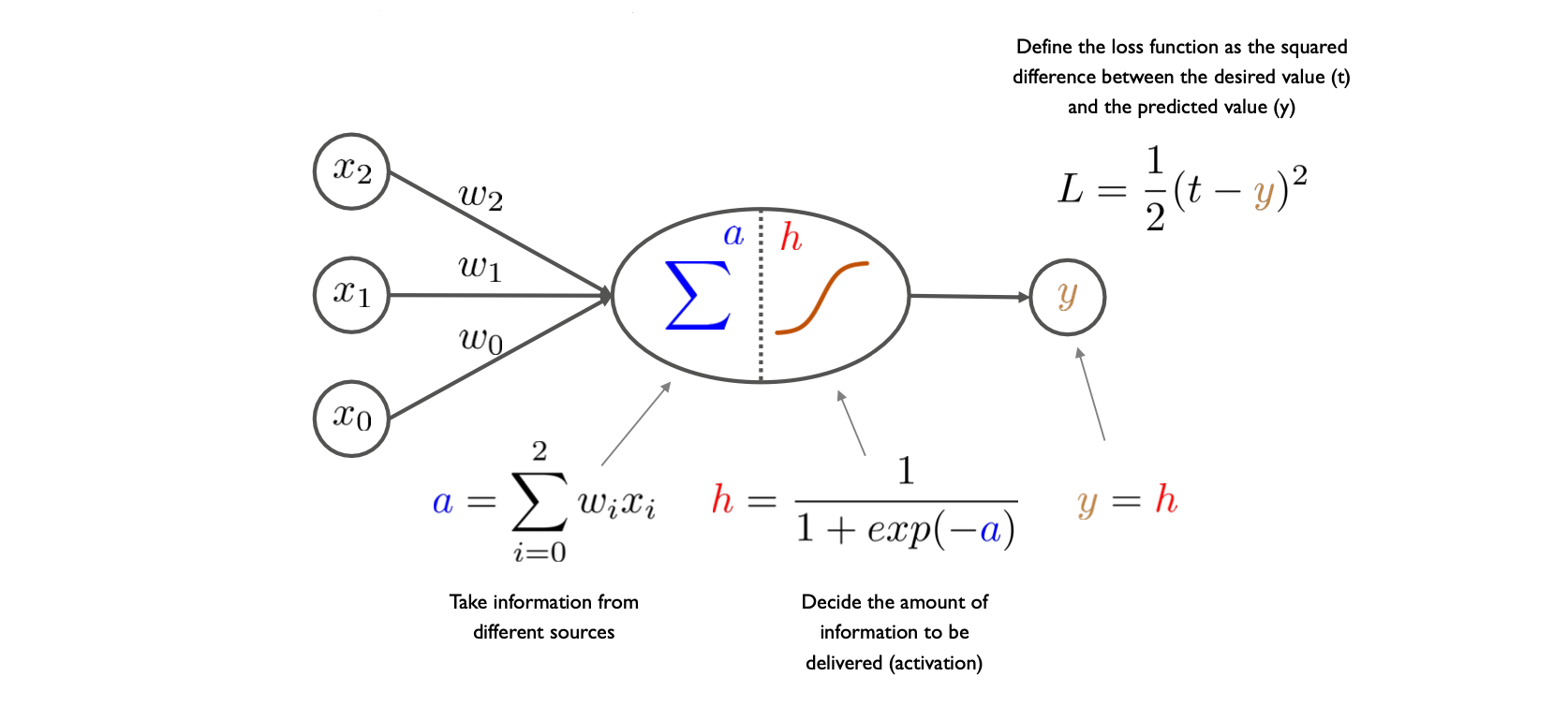
퍼셉트론의 구조는 중앙의 점선에 따라 크게 전반부와 후반부로 나눌 수 있다. 전반부는 이전단계의 정보, 혹은 입력변수를 받는 node 들이고, 만약 사용하는 데이터셋의 설명변수의 수가 5개라면 (bias 까지 추가하여) 6개의 node 가 존재한다. 1개의 샘플의 설명변수에 해당하는 값들은 이 node 들에 들어가며, weight 들과 선형결합하여 하나의 scalar 값을 만든다.
후반부에선 이 scalar 값을 활성화 함수에 넣는다. 활성화 함수 \(h\) 의 특징은 비선형 함수라는 것인데, 만약 이 활성화 함수가 없다면 퍼셉트론은 결국 MLR 과 다름없어진다. 활성화 함수에서 나온 값은 퍼셉트론의 예측값이며, Loss function 에 따라 해당 예측치가 샘플의 실제 값과 얼마나 차이나는지를 정량적으로 평가한다.
위에 서술한 과정은 퍼셉트론의 classification task 의 과정이며, 수학적으론 다음과 같이 표현 할 수 있다.
\[a(\textbf x) = b+\sum_i w_i x_i = b + \textbf w^T \textbf x \\ h(\textbf x) = g(a(\textbf x)) = g(b+\sum_iw_ix_i)\]사람의 뉴런은 다음 뉴런으로 정보를 곧이곧대로 전달하지 않는다. 어느정도 self mechanism 으로 정보의 양을 거르고 다음 뉴런으로 건내기 때문에, 활성화 함수 또한 이를 모방한 것이다. 퍼셉트론에서의 활성화 함수는 다음단계로 전달되는 정보량을 정하는 mechanism 이며, 선형결합으로 이루어진 모델에 비선형 변환을 주기 위해 사용된다.
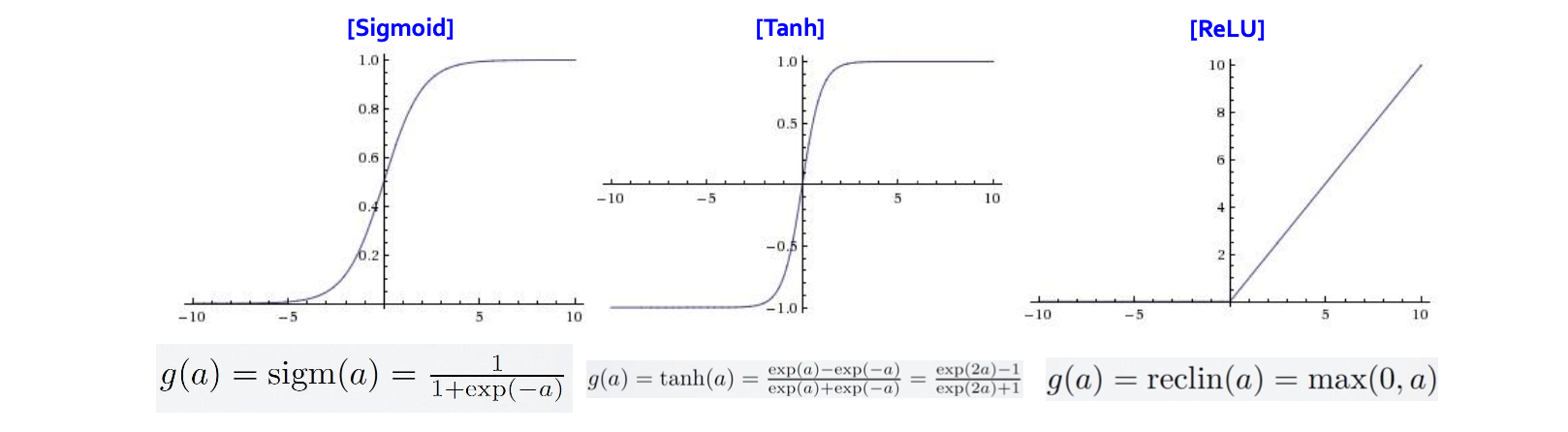
실제로는 다양한 활성화 함수가 존재하지만, 가장 처음 접하는 대표적인 활성화 함수들은 Sigmoid, Tanh (Hyperbolic Tangent), ReLU (Rectified linear unit) 이다.
Sigmoid 함수는 0 과 1 사이의 값을 출력해준다. 가장 고전적인 활성화 함수이지만, 학습속도가 느리다는 단점이 있다. 이에 반해 Tanh 함수는 -1 과 1 사이의 값을 출력해준다. 특점 지점에선 Sigmoid 함수보다 기울기가 두배가 되기 때문에 전반적으로 Sigmoid 함수보다 학습이 빠르다. 하지만 Sigmoid 함수와 Tanh 함수가 가진 단점 중 하나는 vanishing gradient problem 이다.
해당 함수들에선 입력변수가 특정 범위를 벗어나게 되면 해당 점에서 함수의 미분값이 0에 가까워진다. 퍼셉트론의 층을 쌓고 학습을 시킨다면 미분값이 완전히 0에 수렴할 가능성이 생긴다. 이 문제로 인해 ReLU 가 선호된다. ReLU 함수는 이전 두 함수들과 다르게 제곱연산이 없기 때문에 computational complexity 가 낮다. 입력값이 0보다 작으면 0을, 입력값이 0보다 크면 자기 자신을 return 한다는 특징이 있다.
뇌는 사실상 ‘음의 정보’ 를 받지도, 처리하지도 않기 때문에 3개의 활성화 함수 중 실제 뇌와 가장 비슷한 활성화 구조를 가진건 ReLU 라고 할수 있다.
퍼셉트론의 목적은 좋은 binary classifier 을 학습하는 것이다. 이때 실제로 찾아야 하는 변수는 설명변수들과 종속변수간의 관계를 잘 설명하는 \(w\) 이다. 이때 퍼셉트론의 regression 과 classification 에 사용되는 loss function 은 대중적으로 두가지가 사용된다.
\[Regression: \ L = {1 \over 2} (t-y)^2 \\ Classification: \ L = - \sum t_i \ log \ p_i\]Regression 의 loss function 은 앞서 많이 소개된 squared loss 이며, \(t\) 가 실제 target 값이고 \(y\) 가 퍼셉트론이 예측한 값이다.
Classification 의 loss function 은 Cross Entropy Loss 를 많이 사용한다. 퍼셉트론은 binary classifier model 이기 때문에 데이터의 종속변수 값을 먼저 one hot encoding 을 한 뒤, 해당 샘플이 해당 클래스에 속할 확률의 최종 합을 minimize 하는 loss function 이다.
헷갈릴 법도 하지만, Loss function 은 데이터셋의 각 샘플에 대한 손실값이며, Cost function 은 전체 데이터에 대한 model 의 평균 손실값이다.
Gradient Descent
경사하강법은 퍼셉트론의 weight 를 찾는데 가장 처음으로 고안된 알고리즘 중 하나다.
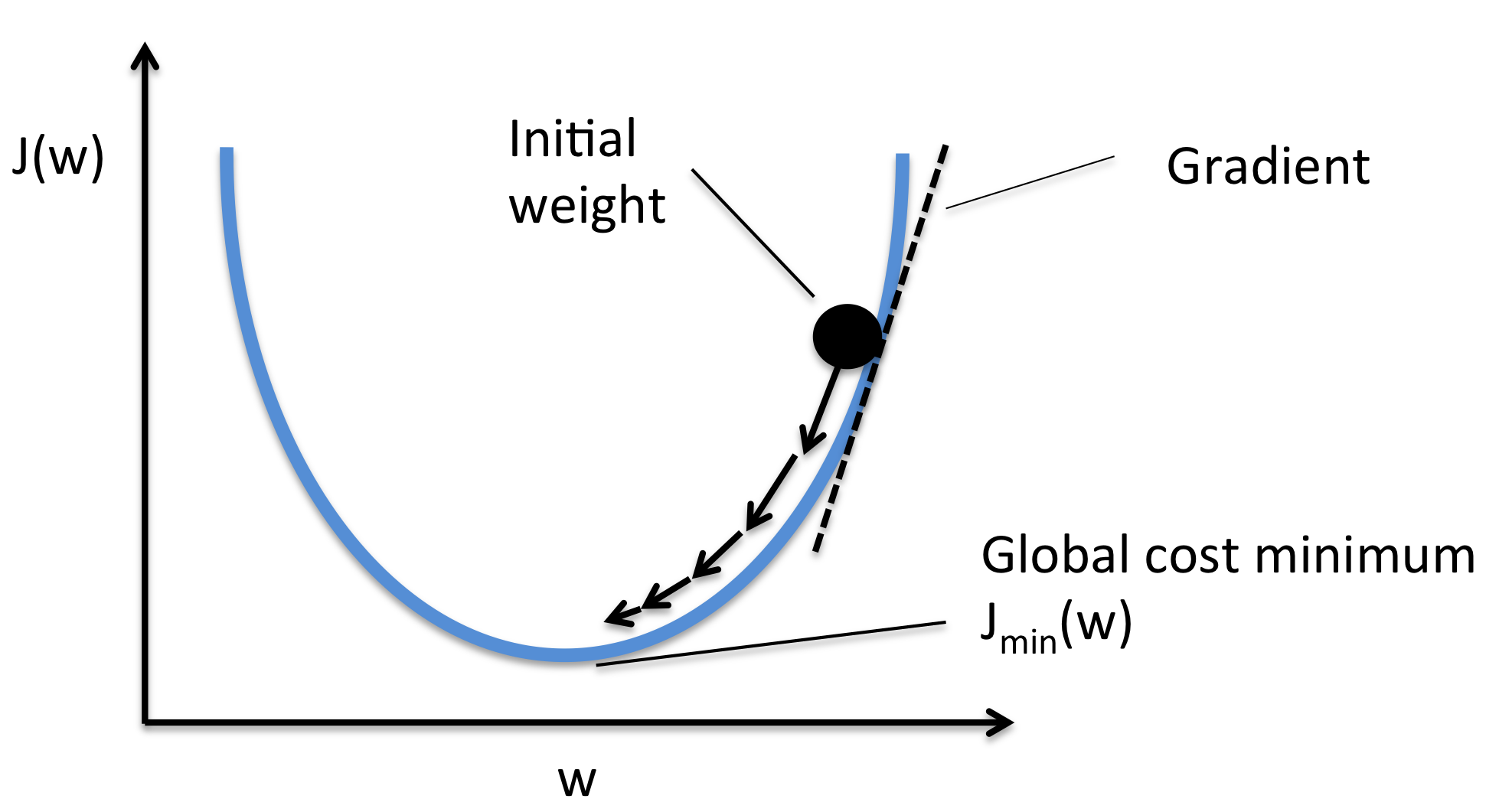
학습의 시작 단계에선 최적의 weight 를 알 수 없으니 random 한 값으로 먼저 initialize 를 한다. 이후 Cost function 의 1차도함수를 구한 뒤, initialize 한 weight 를 1차 도함수에 넣어 기울기를 구한다. 이때 기울기의 반대방향으로 weight 값을 update 하는것이 경사하강법의 핵심이다. Cost function 을 최소화 하는 것이 목적이기 때문에, 해당 weight 의 기울기의 반대 방향으로 움직인다면 Cost function 의 값이 낮아지기 때문이다.
만약 weight 에 대하여 1차 도함수 값이 0이라면 Cost function 의 minima 이기 때문에, 최적의 weight 에 도달했다고 판단하고 알고리즘을 종료 할 수 있다. 하지만 gradient 값이 0이 아니라면, weight 를 gradient 의 반대방향으로 조금 움직인뒤 학습을 진행해야 한다. 이때 얼만큼 움직이는지는 사용자가 직접 지정하는 hyperparameter 이다.
Taylor Expansion and the Chain Rule
테일러 전개 (혹은 급수) 는 미적분에서 배우는 개념이지만, 경사하강법의 이론적인 background 의 역할을 한다. 테일러 급수는 여러번 미분가능한 함수를 특정 점에 대한 멱급수으로 표현하는 방법이다.
\[f(w+\Delta w) = f(w) + {f'(w) \over 1!}\Delta w + {f''(w) \over 2!}(\Delta w)^2 + ...\]만약 \(\Delta w\) 값이 충분히 작다면, 테일러 급수의 2차 도함수 부분부터 0에 수렴하기 때문에 다음과 같이 표현할 수 있다.
\[f(w+\Delta w) = f(w) + {f'(w) \over 1!}\Delta w\]해당 식을 경사하강법의 weight update 관점으로 전개한다면 다음과 같다.
\[w_{new} = w_{old} - \alpha \ f'(w), \ 0 < \alpha < 1\]새로운 weight 는 기존 weight 에서 1차 도함수의 반대방향으로 \(\alpha\) 만큼 움직이는 것이다.
그렇다면 weight 에 대해서 loss function 을 미분해야 하는데, loss function 에는 weight 에 대한 항이 없기때문에 직접 미분이 불가능하다. 그렇기에 Chain rule 을 사용한다. 다음은 regression 에 사용되는 squared error loss function 의 chain rule 이다.
\[{\partial L \over \partial w_i} = {\partial L \over \partial y} \cdot {\partial y \over \partial h} \cdot {\partial h \over \partial a} \cdot {\partial a \over \partial w_i} = (y-t) \cdot 1 \cdot h(1-h) \cdot x_i\]퍼셉트론의 각 단계에 사용되는 함수들을 미분한뒤 chain rule 을 적용시키면 최종적으로 weight 에 대한 loss function 의 미분값을 구할 수 있다. 이 미분값의 반대방향으로 \(\alpha\) 만큼 weight 를 움직여 weight 를 update 하는 것이 핵심이다.
\[w^{new}_i = w^{old}_i - \alpha \times {\partial L \over \partial w_i} = w^{old}_i - \alpha \times (y-t) \cdot 1 \cdot h(1-h) \cdot x_i\]\((y-t)\) 는 만약 실제값과 예측치의 차이가 크다면 weight 많이 update 하는 역할을 하고, \(x_i\) 는 해당 weight 를 update 할 때 해당 설명변수만 영향을 주도록 하는 장치라고 생각할 수 있다. \(\alpha\) 를 Learning Rate 이라 하며, hyperparameter 이기 때문에 사용자가 설정을 한다.
Stochastic, Batch, and Minibatch Gradient Descent
앞서 설명한 경사하강법은 SGD (Stochastic Gradient Descent) 에 해당된다. 이는 datapoint 하나로 weight 를 업데이트 한 뒤 다음 데이터포인트로 넘어가는 방식으로, 세밀한 조정이 가능하지만 오래 걸린다는 단점이 있다.
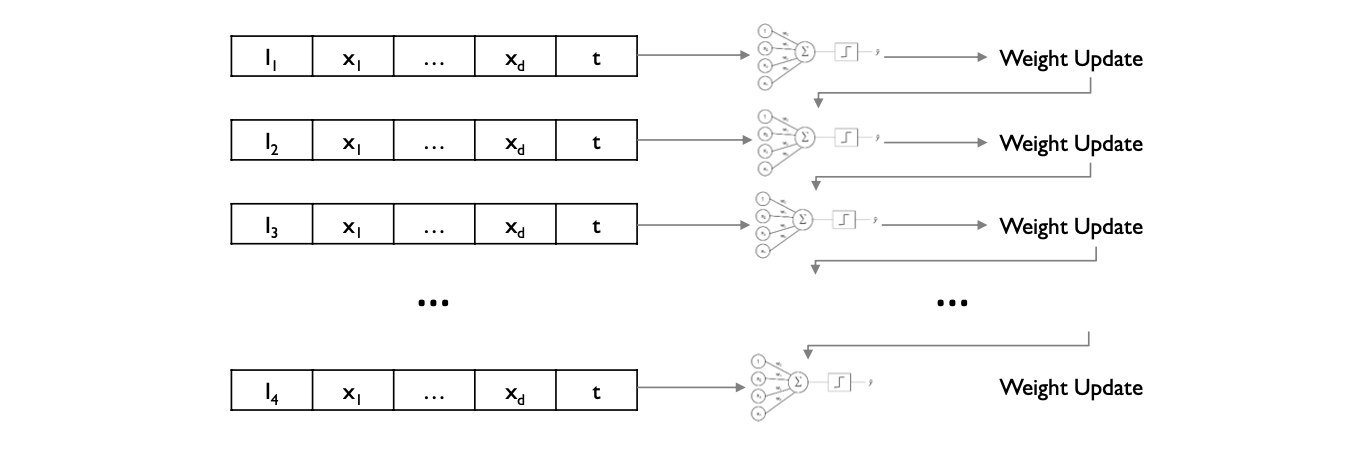
이해 반해 BGD (Batch Gradient Descent) 는 모든 샘플에 대하여 gradient 를 구한 뒤, gradient 의 평균을 통해 weight 를 업데이터 하는 방식이다. SGD 보다 훨씬 빠르지만, SGD 로 학습된 모델보다 성능이 떨어진다는 단점이 있다.
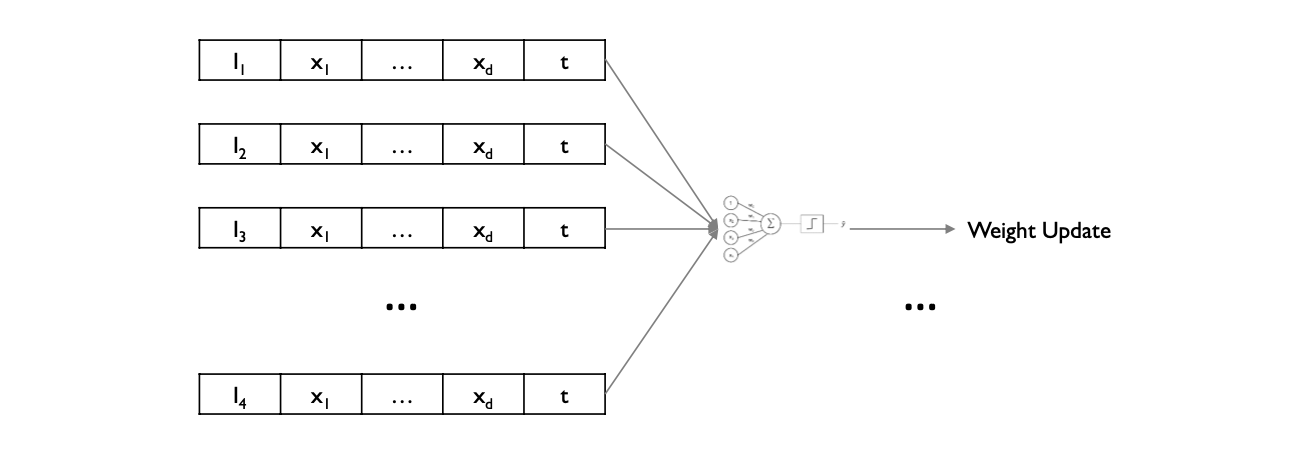
SGD와 BGD 의 절충안을 찾은 알고리즘이 Minibatch GD 이다. 이는 전체 데이터셋을 \(N\) 개의 샘플을 포함한 minibatch 로 나눈 뒤, 해당 batch 속 sample 들로 gradient 의 평균을 구한 뒤 weight 를 업데이트 한다.
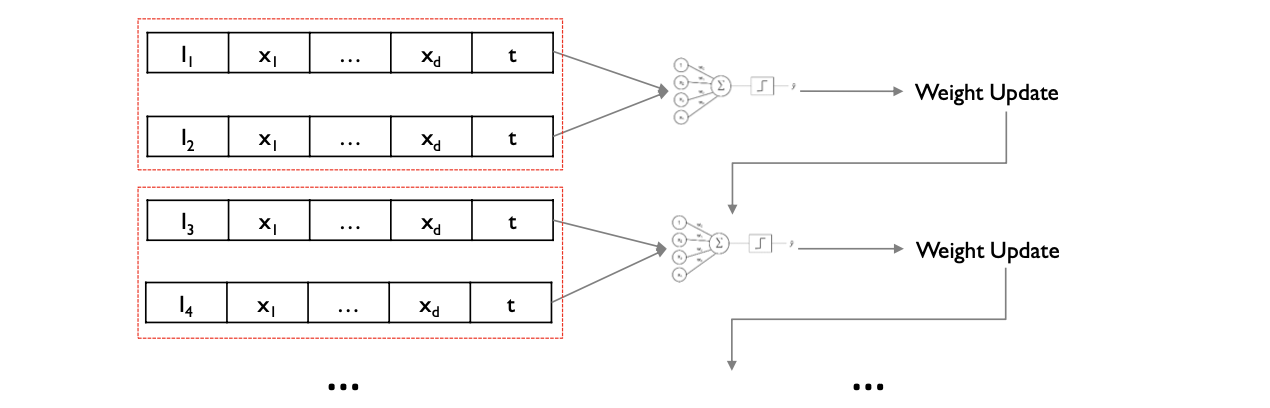
100개의 학습 샘플을 5개의 minibatch 로 나눈 뒤 학습을 1 epoch (학습 데이터셋의 1 full cycle) 진행한다면, 각 알고리즘의 weight update 는 다음과 같다.
SGD = 100 updates
BGD = 1 update
Minibatch = 20 updates
Weight update 에 사용되는 learning rate 를 지정할 때 주의해야 한다. 만약 learning rate 이 너무 크다면, 모델은 converge 하지 않고, 너무 작다면 학습에 너무 오랜 시간이 걸린다.
사실 SGD, BGD, minibatch 는 굉장히 많은 optimizers (학습 알고리즘) 중 기초적인 모델들이다. Optimizing 알고리즘에 대한 연구는 많이 진행되고 있으며, 가장 많이 쓰이는 대표적인 optimizer 는 Adam, RMSProp 이 있다.