Dimensionality Reduction - PCA (Principal Component Analysis)
Contents
- Introduction
- Mathematical Background
- Covariance Matrix
- Projection
- Eigenvalue and Eigenvector
- Principal Component Analysis: PCA
- Step 1: Data Centering
- Step 2: Optimization
- Step 3: Lagrangian Multiplier
- Step 4: Find Bases
- Step 5: Select Bases
Introduction
이전 장에선 차원축소를 위해 중요한 변수들을 선택하는 방법론들인 FS, BE, SS, 그리고 Genetic Algorithm 에 대해 알아보았다. 이번 장에서 다루는 PCA (주성분분석) 는 기존의 변수들의 특징들을 추출하여 새로운 변수들을 만드는 변수 추출법 (Feature Extraction) 이다. PCA 는 선형변환 feature extraction 중 하나이며, 데이터의 속성을 보존하면서 새로운 변수를 생성한다. 선형변환 feature extraction 방법론들은 기존 데이터의 어떠한 특징을 최대한 보존할지에 따라 나뉘는데, PCA 는 기존 데이터의 분산을 최대한 보존하는 기저벡터를 찾아 데이터를 사영시키는 방법론이다.
Dimensionality Reduction 의 간단한 Taxonomy 는 다음과 같다:
- Feature Selection
- Filter
- Information Gain
- Odds Ratio, etc
- Wrapper
- Forward Selection
- Backwards Elimination
- Stepwise Selection
- Genetic Algorithm
- Feature Extraction
- Max. Variance
- PCA (Principal Component Analysis)
- Max. Distance Info
- MDS (Multidimensional Scaling)
- Reveal non-linear structure
- LLE
- ISOMAP
- t-SNE
Mathematical Background
주성분분석을 알아보기 전 선형대수에서 처음 접하게 된 수리적 배경부터 알아보자. 앞으로 나올 행렬연산의 행은 변수고, 열은 데이터의 샘플로 작성하였다.
Covariance Matrix
공분산 행렬은 특정 행렬을 통해 계산할 수 있으며, 해당 행렬의 데이터 구조와 특징쌍에 대한 변동에 대한 중요한 정보를 나타낸다. 행렬의 분산의 정보가 담겨있다 라고 이해할 수 있다.
\[Cov(\mathbf{X}) = {1\over n}(\mathbf{X}- \bar{\mathbf{X}})(\mathbf{X}- \bar{\mathbf{X}})^T\\ Cov(\mathbf{X}_{ij}) = Cov(\mathbf{X}_{ji})\]행렬 \(\mathbf{X}\) 에 대한 공분산 행렬은 위와 같이 계산할 수 있다. 이때 \(\mathbf{X}\) 는 \(d \times n\) 의 행렬이기에 공분산 행렬은 \(d \times d\) 의 dimension 을 갖는다. 공분산 행렬은 대칭행렬이고, 전체 데이터셋의 분산은 공분산 행렬의 trace 라는 특징을 갖는다.
Projection
선형대수에서 배우는 사영은 주성분분석에서 굉장히 중요한 역할을 한다.

\(\vec b\) 와 \(\vec a\) 가 있을 시, \(\vec b\) 의 끝에서 \(\vec a\) 와 직교하는 수선의 발을 내리고 \(\vec a\) 에 대한 해당 수선의 발 까지의 길이를 \(p\) 라고 하자. 그렇다면 \((\vec b - p \vec a)^T\vec a = 0\) 이 될거고, 이를 전개 후 \(p\) 에 대해 정리하면 \(p = {\vec b^T\vec a \over \vec a^T \vec a }\) 가 된다. \(p\vec a = \vec x\) 라고 정의한다면 \(\vec x = p \vec a = {\vec b^T\vec a \over \vec a^T \vec a } \vec a\) 가 된다. 이때 \(\vec a\) 가 기저벡터라면 \(p = \vec b^T\vec a\) 가 되며, \(\vec x = p \vec a = (\vec b^T \vec a)\vec a\) 가 된다.
이때 \(p\) 는 원래 벡터 \(\vec b\) 를 기저벡터 \(\vec a\) 에 사영시킨 후의 scalar 값이 된다.
Eigenvalue and Eigenvector
고윳값과 고유벡터는 주성분분석의 핵심역할을 담당한다.
\[\mathbf{Ax=\lambda x} \rightarrow \mathbf{(A-\lambda I)x}=0\]\(\mathbf{x}\) 라는 벡터에 \(\mathbf{A}\) 라는 선형변환을 취했다. 이때 선형변환 후의 행렬이 scalar 값인 \(\lambda\) 와 기존 \(\mathbf{x}\) 의 곱으로 표현할 수 있다면, \(\lambda\) 는 행렬 \(\mathbf{A}\) 의 고윳값이며 \(\mathbf{x}\) 는 행렬 행렬 \(\mathbf{A}\) 의 고유벡터이다.
만약 행렬 \(\mathbf{A}\) 의 역행렬이 존재한다면 (non-singular matrix 이라면), rank \(d\) 개의 고윳값-고유벡터 쌍이 존재한다. 그리고 이 행렬의 trace 는 고윳값의 합과 같다.
앞서 언급했듯이 전체 데이터셋의 분산은 데이터셋의 공분산 행렬의 trace 와 같다. 해당 공분산 행렬의 역행렬이 존재한다면, 행렬의 trace 는 고윳값의 합이다. 즉, 특정 데이터셋의 전체 분산은 공분산 행렬의 고윳값의 합이다.
추가적인 설명이 필요하다면 공돌이의 수학정리노트 를 참고하자. 명쾌하고 직관적인 설명을 해주신다.
Principal Component Analysis: PCA
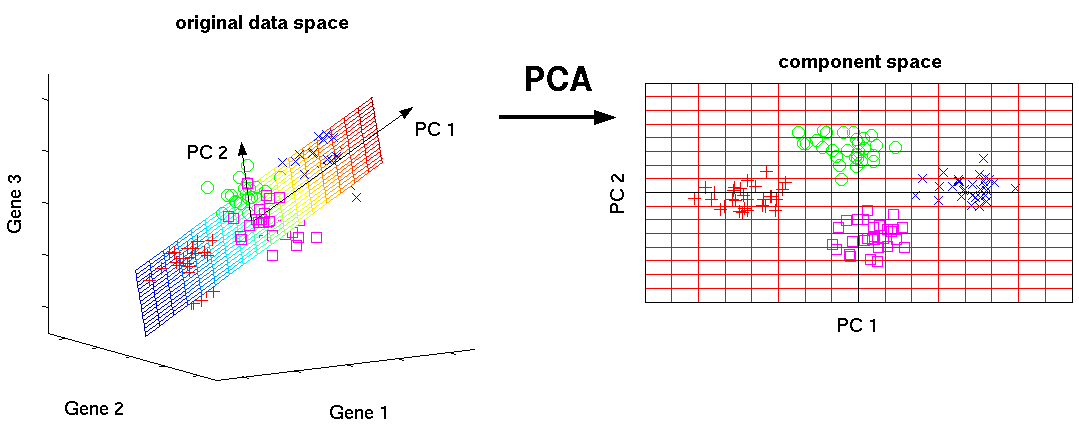
위 예시는 3차원의 데이터를 2차원으로 사영시킨 PCA 의 시각적 예시다. 기존의 데이터는 3차원의 feature space 에 분포가 되어있는데, 데이터의 분산을 최대한 보존시키며 사영을 하니 3차원에서 볼 수 있었던 데이터의 군집이 그대로 2차원에도 표현이 된 것이다.
Purpose: Find a set of orthogonal basis vectors that can preserve the variance of the original data as much as possible after projecting it upon the set.
\(X_1, X_2, ...,X_p:\) Original Variables
\(\mathbf{a}_i = [a_{i1},a_{i2},...,a_{ip}]:\) \(i^{th}\) Basis vector/Principal Component
\(Y_1, Y_2,...,Y_p:\) Variables after the projection onto the \(i^{th}\) Basis Vector
기존 데이터셋에 p개의 변수가 있고, p 개의 변수벡터들을 각각 기저벡터 \(\mathbf{a}_i\) 에 사영하면 scalar 값인 \(Y_i\) 가 나온다. 이때 \(Y_i\) 의 분산을 계산하고, 분산이 최댓값이 되는 기저벡터 \(\mathbf{a_i}\), 즉 주성분을 를 찾는것이 PCA 의 주 목적이다. 이때 몇개의 주성분을 사용할지는 분석가의 선택이다.
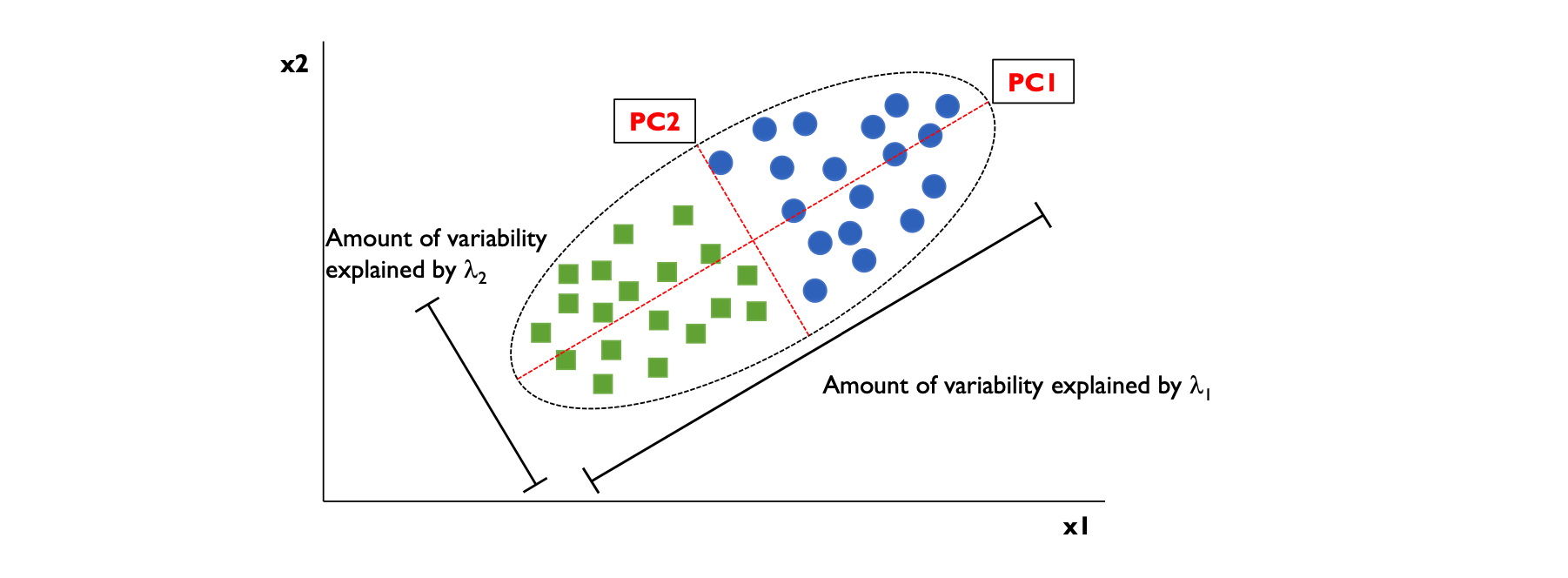
분산이 보존된다는 것은 위 그림을 보면 직관적으로 이해가 가능하다. 데이터셋을 두개의 주성분에 사영시켰을 시, 보존되는 분산의 정도는 \(\lambda_i\) 로 계산할 수 있다.
Step 1: Data Centering
예시를 통해 주성분분석의 작동방식을 살펴보자. 이때 데이터셋은 기존에 사용하는 행렬과 반대로 \(d \times n\) 차원의 행렬로 표현한다 (행에 변수, 열에 샘플).
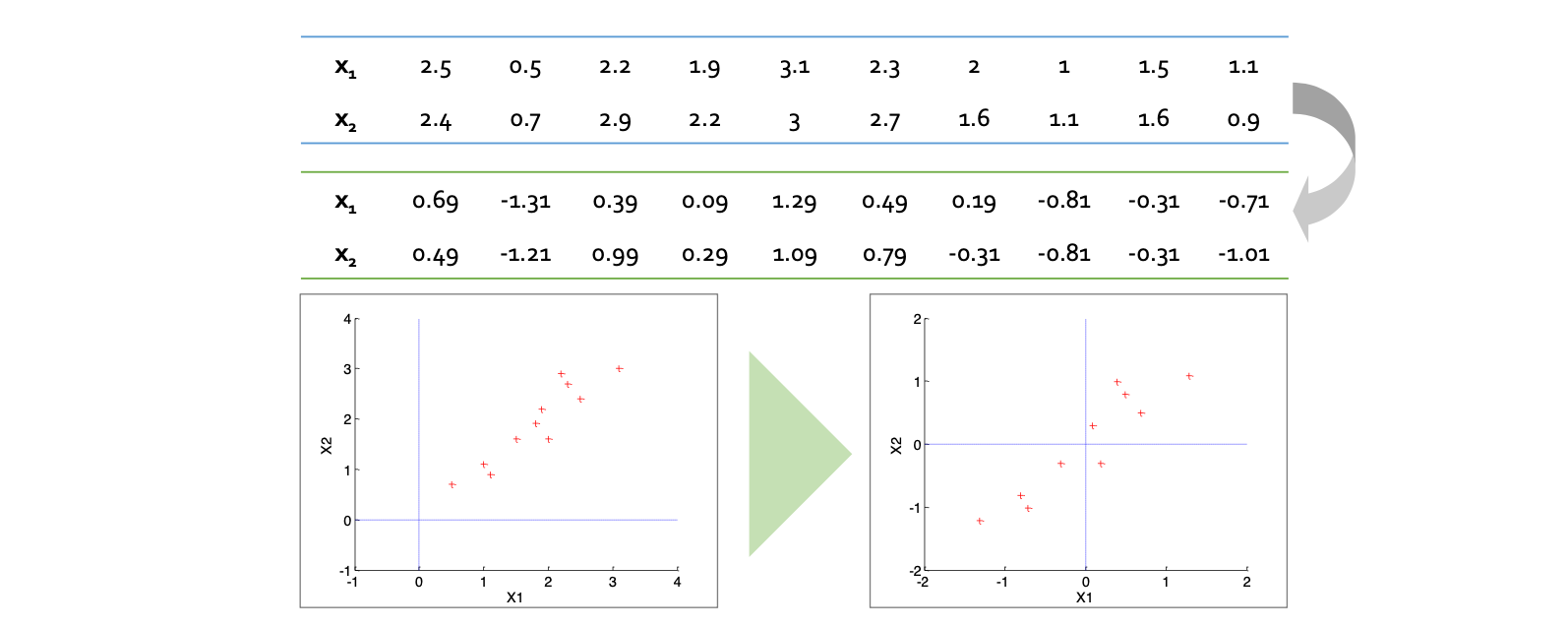
먼저 Data Centering 을 통해 객체들을 평균값으로부터 빼준다 (Normalizing).
사실 Data Centering 단계에 대한 의문이 들었다. 어짜피 공분산 행렬 \(Cov(\mathbf{X}) = {1\over n}(\mathbf{X}- \bar{\mathbf{X}})(\mathbf{X}- \bar{\mathbf{X}})^T\) 는 데이터의 분산의 정보를 나타내기 때문에 Centering 을 하던말던 공분산 행렬은 변하지 않기 때문이다.
How does centering make a difference in PCA (for SVD and eigen decomposition)? 는 같은 의문을 던지는데, 정리하자면 ‘Non Centered Data’ 를 통한 주성분분성이라 함은 공분산 행렬 대신 \(\mathbf{X^T X}/(n-1)\) 행렬로 고윳값분해를 진행하는 방법론이다.
Step 2: Optimization
기존 데이터셋은 \(p\) 개의 변수가 있다. 분산이 최대화 되는 기저벡터 \(w\) 에 변수벡터 \(x\) 를 사영시켜야 하는데, 사영 후의 분산은 다음과 같이 계산 할 수 있다.
\[V = {1 \over n}(\mathbf{w^T X})(\mathbf{w^T X})^T = {1 \over n}(\mathbf{w^T XX^T w}) = \mathbf{w^T Sw}\]기저벡터 \(\mathbf{w}\) 과 전체 데이터셋 \(\mathbf{X}\) 에 대한 scalar 분산 값은 \(V\) 다. 첫번째 항을 잘 보면 공분산 행렬을 구하는 공식과 닮아있다. 이를 전개하고 공분산 행렬의 식이 \({1\over n}\mathbf{XX^T}\) (Normalize 하였다는 전제하에) 인 것을 기억하자. 이를 sample 공분산 행렬 \(\mathbf{S}\) 라고 치환하면 분산을 마지막 항인 \(\mathbf{w^T Sw}\) 로 표현 할 수 있다.
주성분분석은 사영 후의 분산값의 최대화 이기 때문에, 다음과 같은 모델링으로 표현 할 수 있다.
\[\mathbf{max \ w^T Sw}\\ \mathbf{s.t. \ w^T w}=1\]Step 3: Lagrangian Multiplier
위의 최적화 문제는 제약식에 strict equality 가 존재하므로, 라그랑주 승수법을 사용한다.
\[\mathcal{L} = \mathbf{w^T Sw - \lambda (w^T w-1)}\\ {\partial \mathcal{L} \over \partial \mathbf{w}} = 0 \Rightarrow \mathbf{Sw - \lambda w} = 0 \Rightarrow (\mathbf{S-\lambda I})\mathbf{w} = 0\]즉, 기저벡터 \(\mathbf{w}\) 에 대한 1차도함수가 0이 되는 지점으로 편미분을 진행한다면 해는 위에서 구한 sample 공분산 행렬의 고윳값과 고유벡터로 표현 할 수 있다. 구하고자 하는 기저벡터가 sample 공분산 행렬의 고유벡터가 되는 것이다.
Step 4: Find Bases
첫 단계에서 두개의 변수를 가진 데이터셋을 다시 예시로 들자면, 두개의 고유벡터-고윳값 쌍이 구해진다. 이때 고윳값을 내림차순으로 정리한 뒤 해당 고유벡터를 기저로 사용하면 된다.
데이터를 첫번째 기저벡터에 사영한다면, 분산은 다음과 같이 계산할 수 있다.
\[V = {1 \over n}(\mathbf{w_1^T X})(\mathbf{w_1^T X})^T = {1 \over n}(\mathbf{w_1^T XX^T w_1}) = \mathbf{w_1^T Sw_1}\\ \text{since} \ \mathbf{Sw_1} = \lambda_1 \mathbf{w_1}, \ \mathbf{w_1^T Sw_1} = \mathbf{w_1^T \lambda_1 w_1} = \lambda_1 \mathbf{w_1^T w_1} = \lambda_1\]즉, 데이터를 고유벡터인 기저벡터 \(\mathbf{w_1}\) 에 사영한다면 데이터의 분산은 고윳값인 \(\lambda_1\) 이 된 다.
Step 5: Select Bases
기저벡터들과 보존되는 분산의 양을 찾았다면 몇개의 기저벡터들을 사용할지 정해야 한다. 이때 closed form solution 은 존재하지 않으므로 데이터의 분산을 얼만큼 보존하고 싶은지에 따라 cutoff 를 정할 수 있다.
데이터셋에 대한 분산은 고윳값의 총합이기 때문에, 하나의 기저에 데이터를 사영 시 보존되는 분산의 양은 다음과 같이 계산할 수 있다.
\[{\lambda_k \over \lambda_1 + \lambda_2 + ... + \lambda_d}\]보통 사용하는 주성분의 개수가 늘어날수록 보존되는 분산의 양이 급격히 감소한다. 이에 따라 Scree Plot 을 도식하여 elbow point 에 따라 cutoff 를 정할 수 있고, 전체 데이터에 대한 cutoff 를 정하고 싶다면 Cumulative variance plot 을 그려 cutoff 를 정한다.
데이터셋이 가우스 분포를 따르고 있지 않다면 주성분분석의 성능이 급격히 낮아진다는 치명적인 단점이 있다. 통계에서 출범된 방법론이기 때문에 현실 데이터셋에 실용적인 적용을 못 할 수 있지만, 이에 따라 FLDA 같은 방법론이 발전하였다.
정리:
PCA 의 목적은 데이터가 가지고 있는 특징을 분산으로 정의하여, 원 데이터의 분산을 제일 잘 보존하는 소수의 기저 (주성분)을 찾아 원 데이터를 이에 사영시켜 차원축소를 하는 방법론이다.
해당 포스트는 강필성 교수님의 Business Analytics 를 참고하여 작성되었습니다.