Multiple Linear Regression
Contents
- Multiple Linear Regression
- Ordinary Least Square
- Sum-of-Squares Decomposition
- Evaluating Regression Models
해당 포스트는 2021년 1학기 고려대학교 강필성 교수님의 ‘다변량분석’ 강의를 참고하여 작성되었습니다.
이미지는 강필성 교수님의 강의 슬라이드에서 발췌하였습니다.
A+ 감사했습니다 교수님
Multiple Linear Regression
다중선형회귀분석은 역사가 오래된 통계적 기법으로, 정량적 종속변수와 설명변수들의 집합간의 선형 관계식을 찾는 기법이다.
위 첫번째 식이 데이터셋을 실제로 설명하는 회귀식이고, 두번째 식이 다중선형회귀분석을 통해 추정된 회귀식이다. 종속변수는 설명변수들의 1차항의 결합으로 표현할 수 있고, 첫번째 식의 epsilon 은 실제 데이터에서 볼 수 있는 변동성, 혹은 noise 라고 한다.
다중선형회귀분석을 진행하는 이유는 크게 두가지로 나눌 수 있다.
| Explanatory Regression | Predictive Regression | |
|---|---|---|
| 목적 | 종속변수와 설명변수간의 관계를 설명 | 미래 데이터를 예측하기 위한 회귀식 추정 |
| 목표 | 각 설명변수의 회귀계수 \(\beta\) 추정 | 미래 데이터 예측 |
| 방법론 | Goodness of fit, \(R^2\), Residual Analysis, p-values | 학습 데이터셋으로 모델학습 |
| 분석대상 | \(\hat \beta\) | \(Y\) |
즉 Explanatory Regression 은 통계적 기법이고, Predictive Regression 은 머신러닝적 기법이다.
Ordinary Least Square
OLS (Ordinary Least Square) 기법, 혹은 최소자승법은 Explanatory Regression 에서 \(\hat \beta\) 를 구하는데 사용하는 기법 중 하나이며, 가장 대중적인 방법론이다.
OLS 는 실제값과 추정치의 차이의 제곱합을 통해 구한다. 부호를 상쇄시키기 위해 절댓값의 합과 제곱합 두개의 선택지가 있지만, 절댓값은 미분이 불가능하다는 점에서 OLS 가 가장 많이 쓰인다. 위 식이 어떻게 계산되며 어떤 결과물이 확 와닿지 않지만, 행렬연산을 통해 시각화하면 이해가 간다.
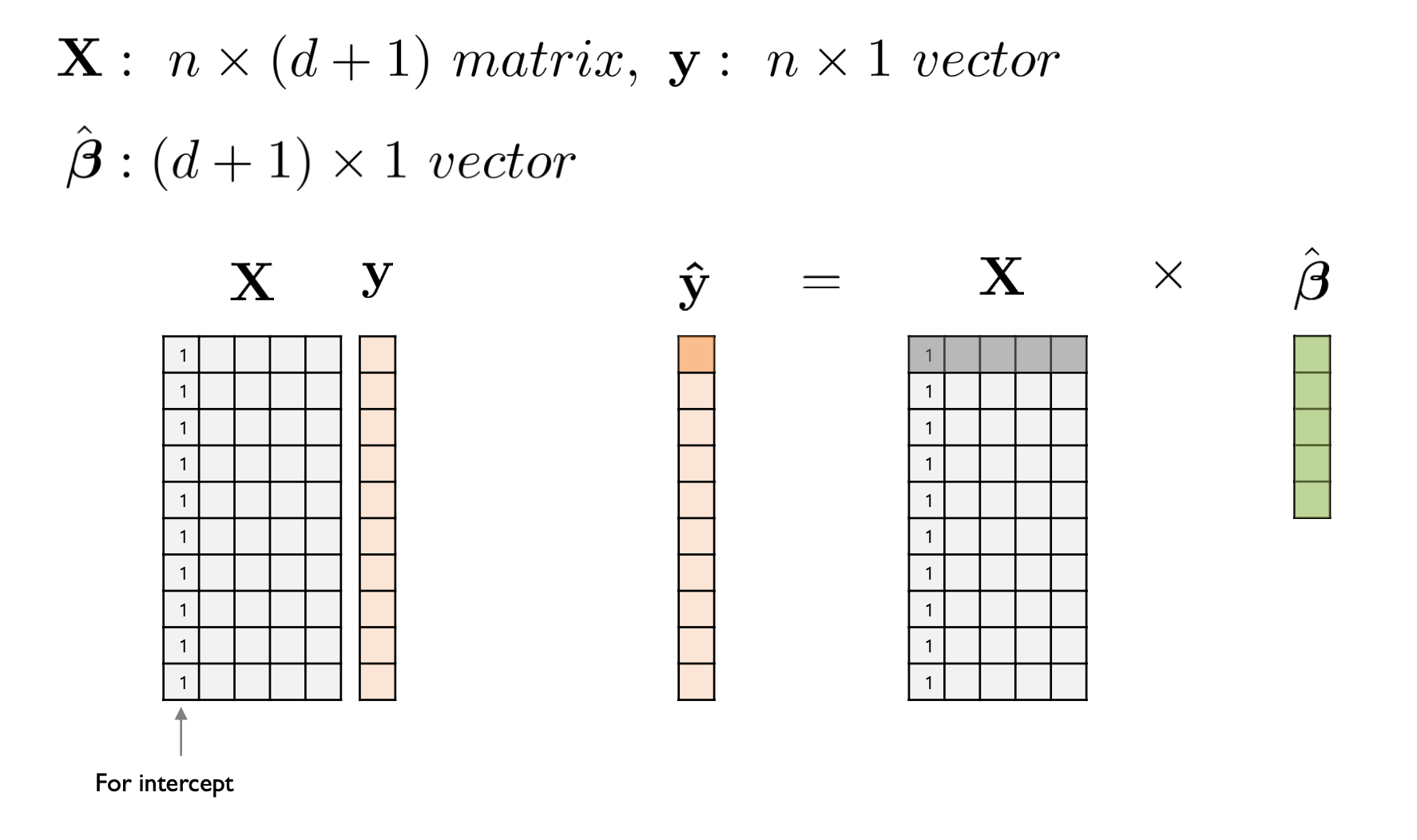
X 는 설명변수이고, y 는 종속변수다. 이때 X 의 크기는 n x d+1 이며, +1 을 해주는 이유는 선형회귀식의 상수항 \(\hat\beta_0\) 을 표현하기 위함이다. 그렇기 때문에 X 의 첫번째 열은 전부 1로 채워진다.
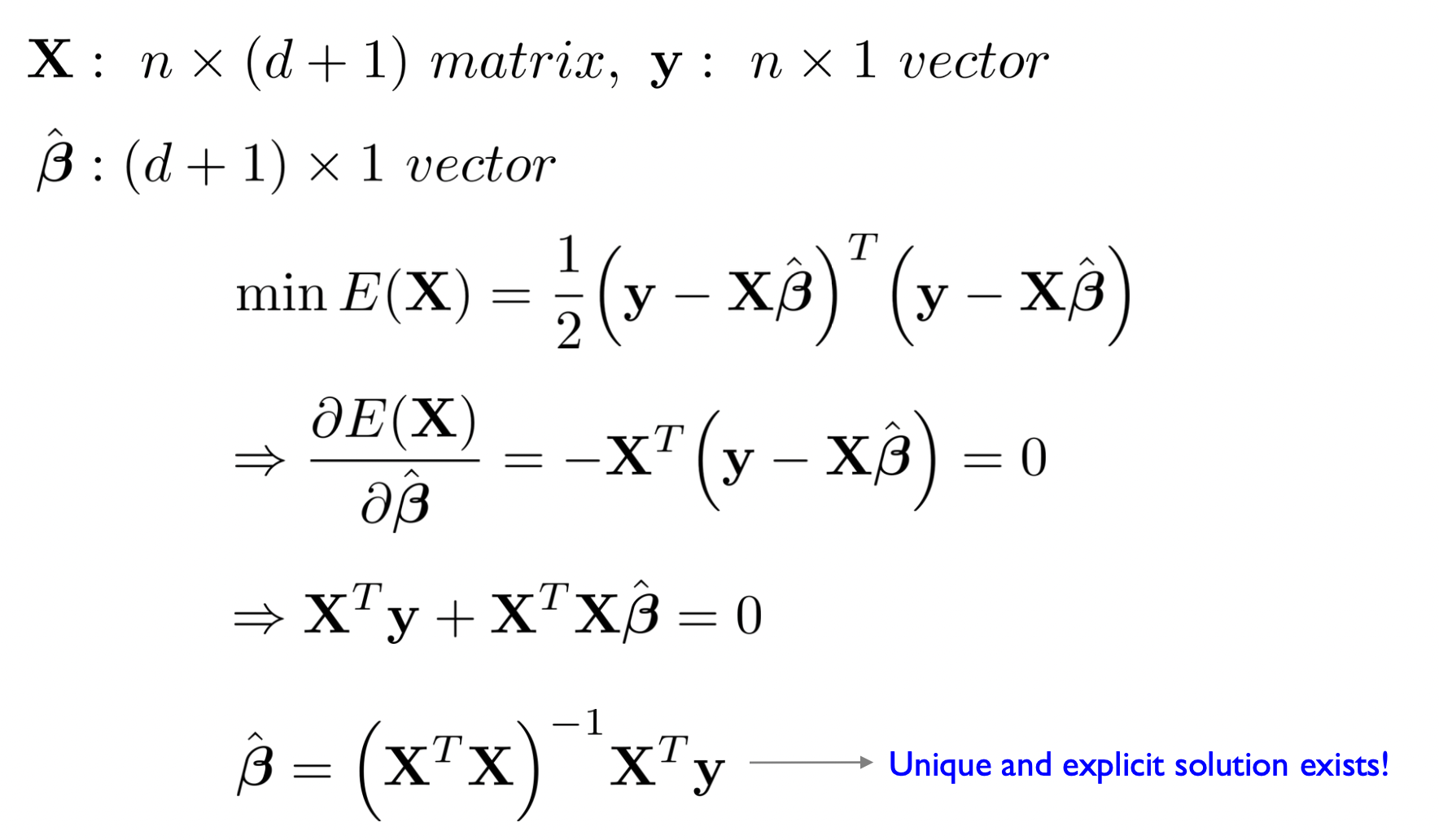
\(\hat y\) 은 \(X\hat\beta\) 이기 때문에 위와 같이 쓸 수 있다. Minimize을 하기 위해 OLS 의 결과는 scalar 값이 나와야 하기 때문에, 앞의 행렬의 전치행렬을 곱해준다. 이후 Min 값을 구하기 위해 \(\hat \beta\) 에 대해 양변을 편미분해주면 그 값은 0이 나와야하기 때문에 \(\hat \beta\) 에 대해 정리를 해주면 다음과 같은 행렬연산식을 얻을 수 있다.
\[\hat\beta = (X^TX)^{-1}X^Ty\]위 행렬연산을 통해 \(\hat \beta\) 라는 d+1 x 1 행렬을 구할 수 있으며, 해당 행렬이 데이터셋의 회귀계수다. 이는 dataset 을 가장 잘 설명하는 회귀식이 유일하게 하나만 명시적으로 존재한다는것을 의미한다. 즉, OLS 는 우리가 익숙한 머신러닝적 기법을 통한 weight update 방식이 아닌, explicit solution 이 존재하는 기법이다.
하지만 OLS 를 통해 \(\hat \beta\) 를 구할 때, 다음과 같은 조건을 만족해야만 구한 \(\hat \beta\) 이 best estimate 이란 것을 보장할 수 있다.
- \(\epsilon\) follows the normal distribution.
- The linear relationship is correct.
- The cases are independent from each other.
- Homoskedasticity - The variability in Y values for a given set of predictors is the same regardless of the values of the predictors.
1번, 4번 조건을 잔차도를 통해 판단하는 기법은 다음과 같다.
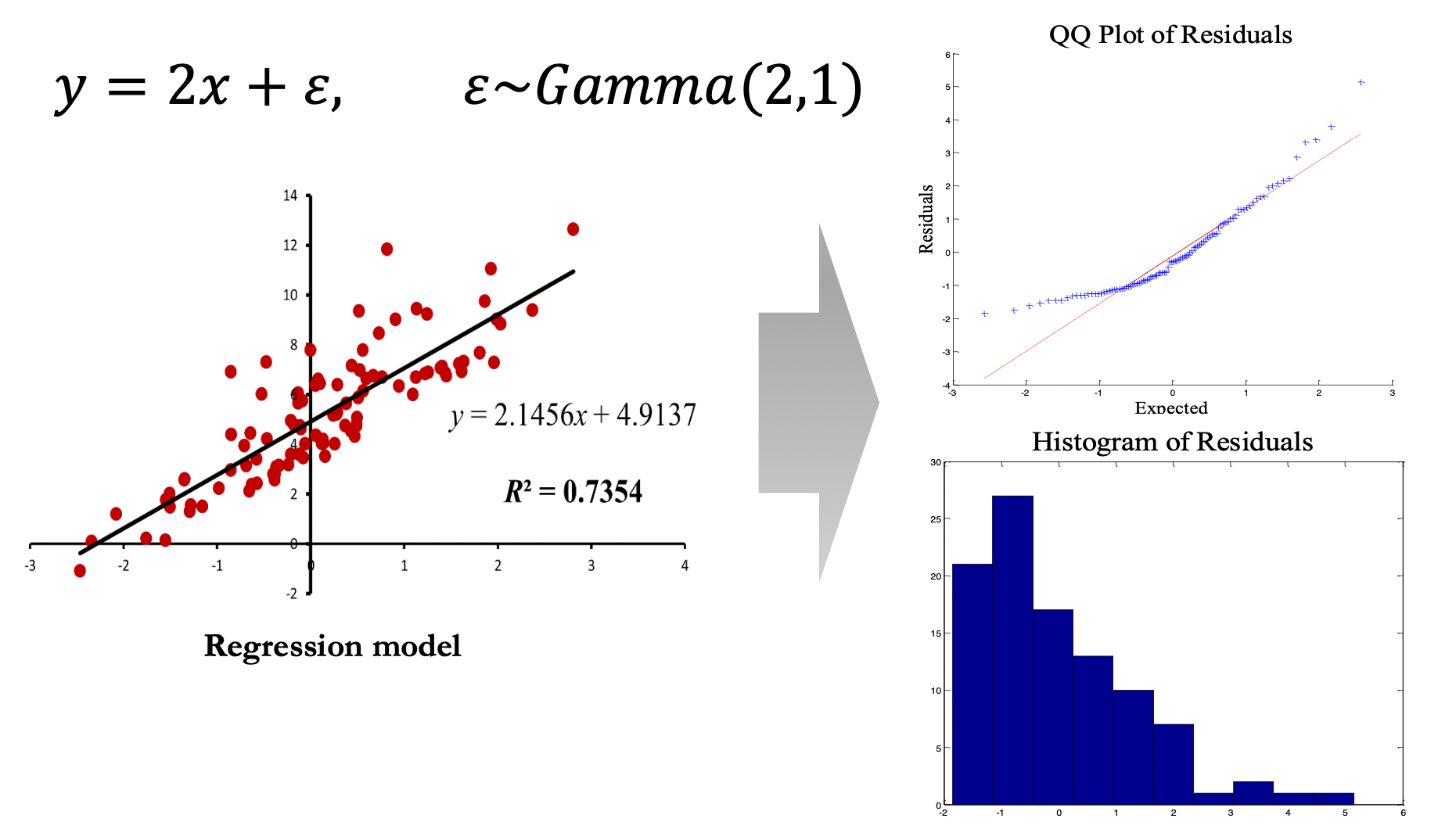
위의 예시를 보자. 실제 데이터는 \(y=2x+\epsilon\) 의 선형관계가 있고, 회귀분석을 통해 \(y=2.1456x + 4.9137\) 란 선형회귀식을 구했다. 이때 선형회귀식과 실제 데이터 사이의 차이를 잔차라고 하는데, 이 잔차 (\(\epsilon\)) 는 정규분포를 따라야 한다. 이를 확인하기 위해 일반적으로 QQ Plot of Residuals 라는 것을 그린다. 해당 plot 의 x 축은 정규분포의 \(\sigma\) 를 나타낸다. 그렇기 때문에 QQ Plot 의 중앙선에서 잔차들이 신뢰구간 95% 이전부터 벗어난다면, 잔차들은 정규성을 띄지 않는다고 판단할 수 있다. Best practice 론 x 축에서 \(\pm2\) 구간 내에 잔차들이 이탈하지 않는다면 정규성을 띈다고 가정한다.
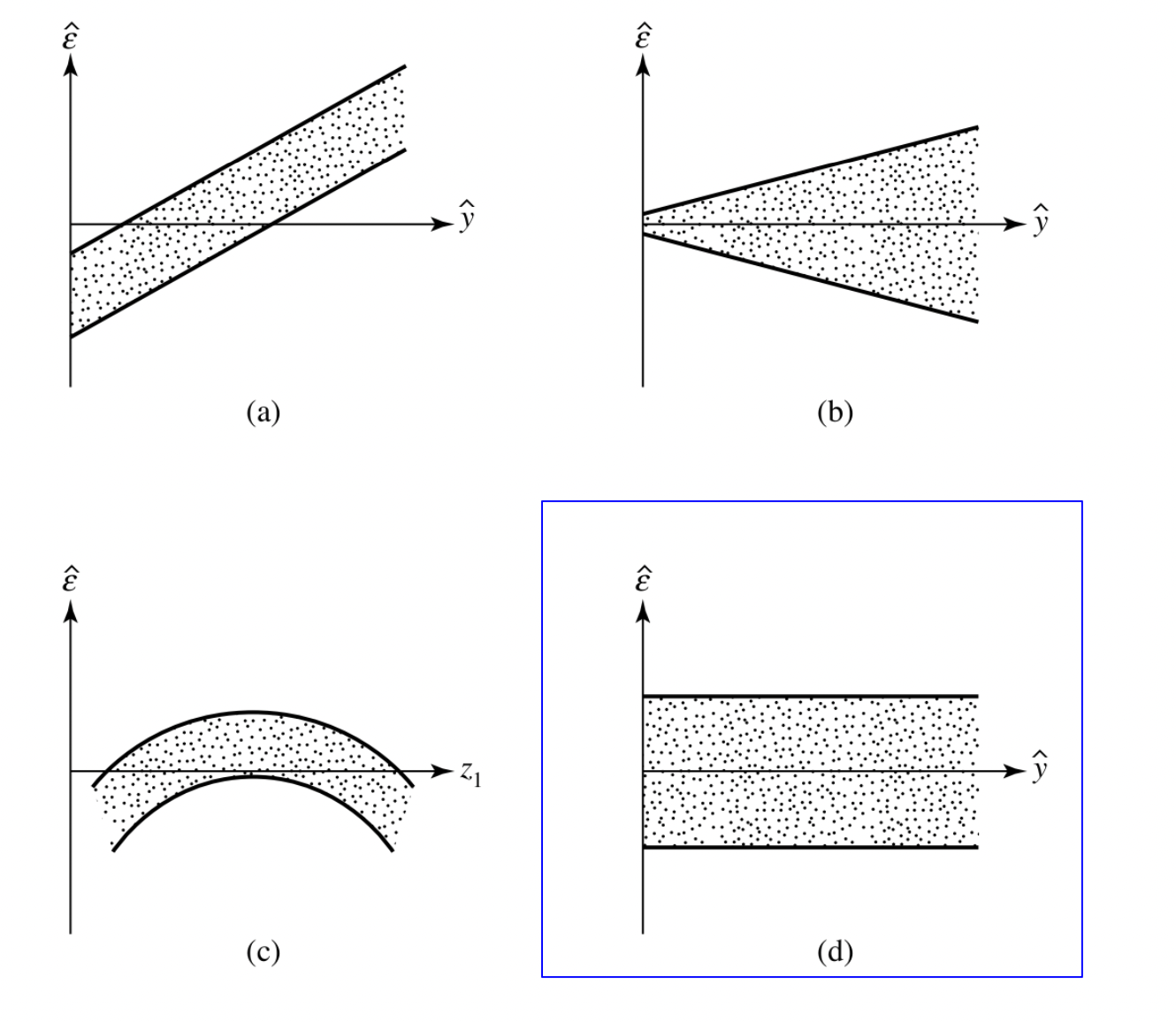
Homoskedasticity 를 확인하는 법은 위의 예시를 통해 이해할 수 있다. x 축에 회귀식으로 예측한 \(\hat y\), y 축엔 잔차를 도식해보면 \(\hat y\) 값의 크기와 상관없이 잔차가 일정한 예시는 d 밖에 없다. 즉, 위 예시 중 Homoskedasticity 조건을 만족하는 회귀식은 d 다.
Sum-of-Squares Decomposition
OLS 를 통해 회귀식을 추정한 뒤, 해당 회귀식의 성능이 얼만큼 좋은지에 대한 정량적인 지표를 ‘Goodness of Fit’ 이라 한다. 이 Goodness of Fit 의 지표 중 하나인 \(R^2\) 을 구하기 위해 먼저 Sum of squares decomposition 을 이해해야 한다.
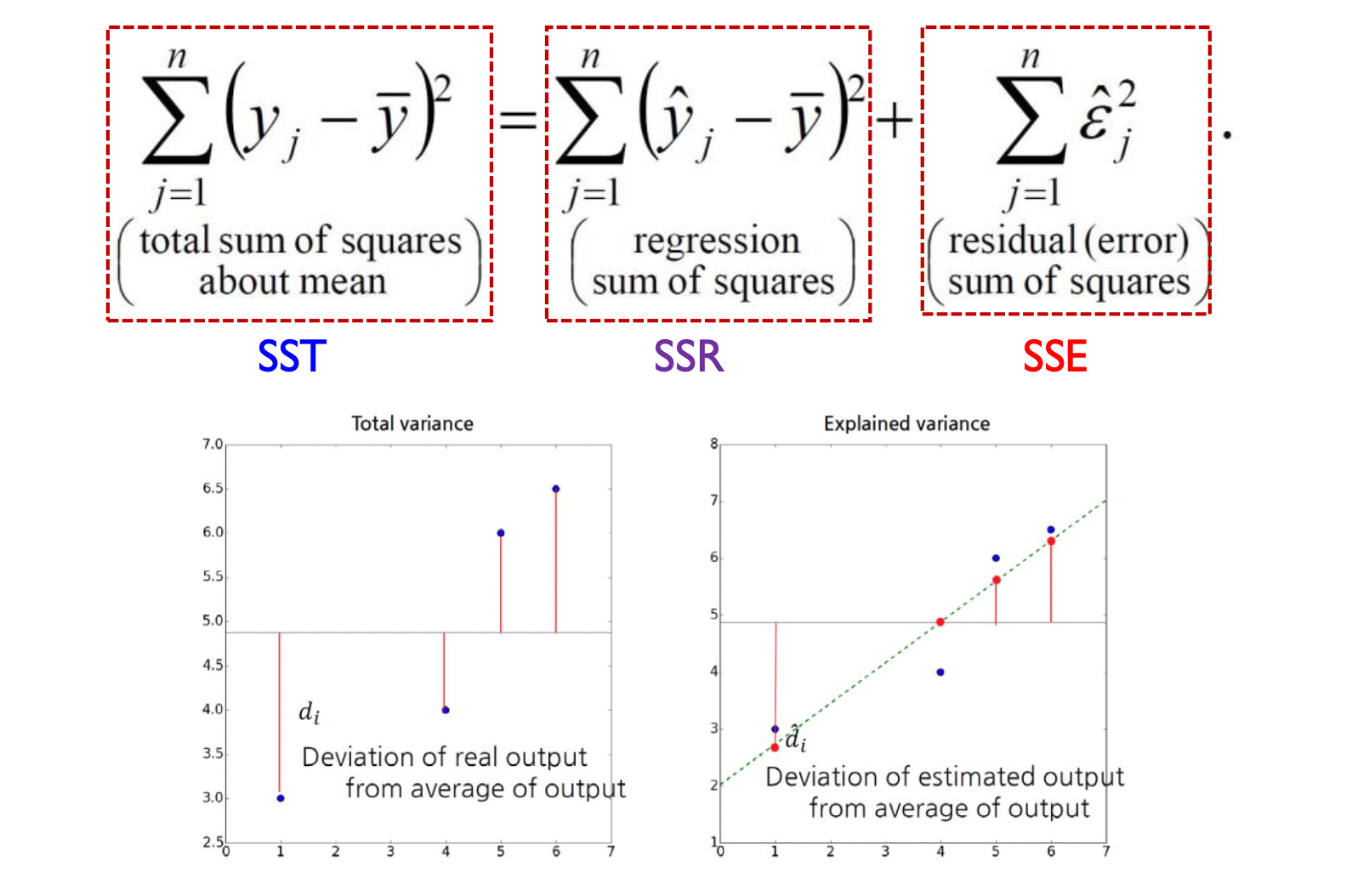
| SST (Sum of Squares Total) | SSR (Sum of Squares Regression) | SSE (Sum of Squares Error) |
|---|---|---|
| 실제값과 평균의 차의 제곱합 | 추정값과 평균의 차의 제곱합 | 실제값과 추정값의 제곱합 |
OLS 로 \(\hat \beta\) 를 구할 때 실제값과 추정값의 제곱합을 최소화하는 조건으로 \(\hat \beta\) 가 구해진다. 반면 SST 는 실제 데이터 값과 실제 데이터 값의 평균의 차로 계산되기 때문에 구해진 \(\hat \beta\) 값이 어떻든 변하지 않는다. 그렇기에 OLS 를 통해 구한 \(\hat \beta\) 값의 성능이 좋다면, SSE 는 작을 것이고 SSR 의 값은 클것이다. 이 원리로 해당 모델의 성능을 평가하는 것이다.
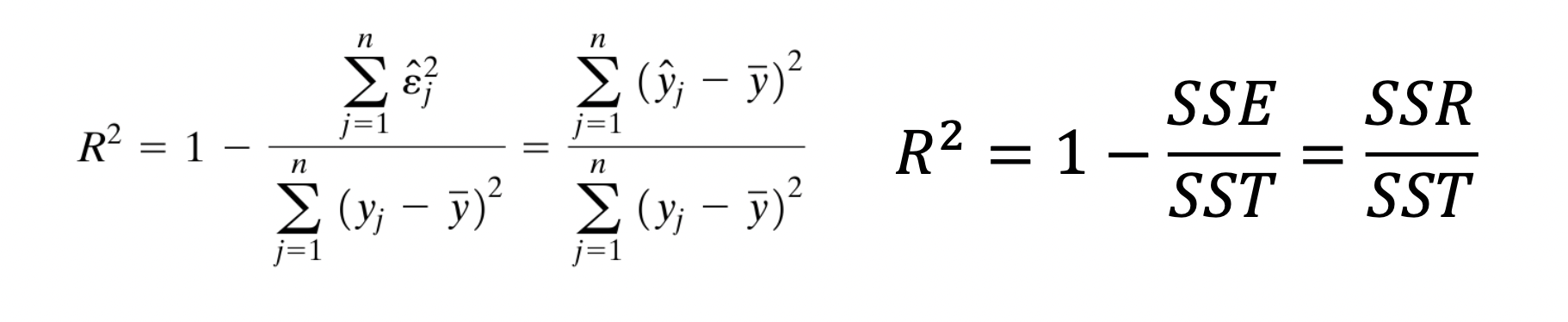
Sum of Squares decomposition 으로 구한 회귀식의 평가지표중 하나인 \(R^2\) 을 구할 수 있다.
- \[0 \leq R^2 \leq 1\]
- \(R^2=1\) 일때 구한 회귀식이 모든 데이터포인트를 지난다
- \(R^2=0\) 일때 설명변수와 종속변수간 그 어떤 선형적인 관계가 없다.
\(R^2\) 값을 구했을 때 값이 높다는건 분석가가 일을 잘했다는 것을 의미하는게 아니다. 앞서 언급하였듯이 하나의 데이터셋으로 구한 \(\hat \beta\) 는 closed form solution 이기에 항상 같은 결과가 나오기 때문에 \(R^2\) 값도 동일하다. \(R^2\) 값이 높게 나왔다면 \(X\) 와 \(y\) 간 선형적 관계가 강하다는것을 의미할 뿐이다.
\(R^2\) 값은 구한 선형회귀식의 좋은 평가지표이지만, 치명적인 단점이 존재한다. 만약 데이터셋의 설명변수의 개수를 늘린다면 설명변수의 실제 설명력과 관계없이 \(R^2\) 값은 단조증가하기 때문이다. 그렇기에 분석이 잘 된것이라 오해하기 쉽다. 이 문제를 해결하기 위해 Adjusted \(R^2\) 을 사용한다.
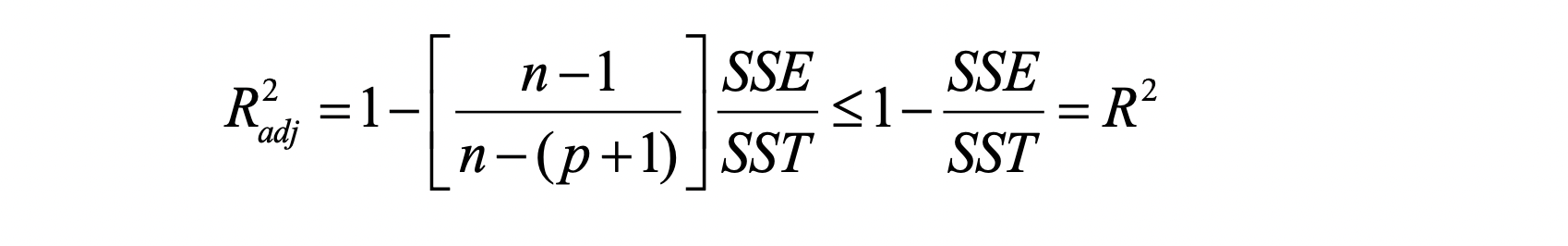
Adjusted \(R^2\) 값을 구하는 식엔 필요 없는 설명변수가 추가될때를 대비한 일종의 장치가 마련된것을 볼 수 있다. \(p\) 는 변수의 수를 의미하며, 종속변수를 설명하는데 있어 insignificant 한 설명변수가 추가된다면 \(p\) 가 +1 이 되며 \(R^2\) 값은 증가하지 않는다. 반대로 말해서 변수를 추가해서 얻는 이득이 확실할때만 \(R^2\) 값이 증가한다.
Evaluating Regression Models
OLS 를 통해 선형회귀식을 구하고, QQ plot of Residuals 를 통해 잔차의 정규성을 검증하고, Homoskedasticity 를 검증한 뒤 \(R^2\) 와 각 변수에 대한 p-value 를 구한다. 이후 Evaluating Regression Models 의 AE, MAE, MAPE, MSE, RMSE 를 접하는데, 처음 다중선형회귀분석을 접했을 때 가장 헷갈렸던 부분이다. 선형회귀식의 성능을 검증하는 부분인데, 앞서 \(R^2\) 값과 p-value 가 이미 성능을 검증하는데 사용되는 지표라고 배웠기 때문이다.
결론부터 말하자면 Sum of Squares Decomposition 으로 구한 \(R^2\), p-value, 그리고 잔차도 검증은 Explanatory Regression 에서 사용되는 고전적인 통계학적 성능평가지표이고, MAE, MSE 등등은 Predictive Regression 에서 사용되는 머신러닝적 성능평가지표이다. 어떠한 관점에서 다중선형회귀를 진행하는지에 따라 용도가 달라지며, MAE, MSE 는 다른 머신러닝 모델 (ex. Random Forest, AdaBoost, SVM Regressor 등) 과 회귀모델의 성능을 비교하는데 사용된다. 즉, \(R^2\), p-value 는 다중선형회귀분석의 범주 내에서의 성능을 평가하는데 사용되며, MAE, MSE 는 다른 회귀모델과 성능을 비교하는데 사용된다.
그렇기 때문에 단락의 이름이 Evaluating Multivariate Linear Regression Models 가 아닌 Evaluating Regression Models 이다. 다른 Regression Models 에도 사용할 수 있는 다용도의 평가지표를 소개하기 때문이다.
Average Error
\[{1 \over n}\sum (y_i - \hat y_i)\]첫번째 평가지표는 Average Error 이다. 실제 값과 예측값의 차이의 합의 평균이다. 부호의 효과 때문에 회귀모델의 성능이 좋다는 착각에 빠지기 쉽기 때문에 사용되지 않는다.
Mean Absolute Error (MAE)
\[{1 \over n} \sum |y_i - \hat y_i|\]MAE 는 Average Error 에 절댓값을 씌운 평가지표다. Average Error 보다는 괜찮은 지표이지만 두개의 회귀모델을 비교할 때 relative difference 를 보여주긴 어렵다.
Mean Absolute Percentage Error (MAPE)
\[{1 \over n} \sum |{y_i - \hat y_i} / y_i|\]MAPE 는 MAE 의 단점을 보완해준다. 실제값과 예측값의 차이를 실제값으로 나눠줌으로써 실제 값에서의 오차를 나타내준다. 그렇기 때문에 QC 같은 상대적 오차가 절대적 오차보다 중요한 분야에서 많이 쓰인다.
Mean Sqared Error (MSE), Root Mean Squared Error (RMSE)
\[MSE = {1\over n} \sum (y_i - \hat y_i)^2 \ , \ RMSE = ({1\over n} \sum (y_i - \hat y_i)^2)^{1/2}\]MSE, RMSE 는 부호를 상쇄시키기 위해 절댓값을 사용한 앞선 지표들과 달리 제곱합을 사용한다. MAE, MAPE 는 실무적인 관점에서 직관적인 이해가 용이하지만 모든 점에서 미분 불가하기 때문에 Analytically untractable 하다. 그렇기에 연구목적에서는 MSE, RMSE 를 더 많이 사용한다. 참고할 점은 사용한 데이터셋이 정규분포를 따르고 극단적인 outlier 가 없다면 RMSE 와 MAE 값은 근사한다.
MAE, MAPE, MSE, RMSE 모두 다른 회귀모델과의 비교를 위해 좋은 평가지표이지만, 상황에 따라 어떤 성능평가지표를 사용하는지는 분석가의 역량이다.