Markov Chain Monte Carlo Algorithm

Bayesian Inference - Frequentism vs. Bayesianism
Likelihood and Maximum Likelihood Estimation
Rejection Sampling
- Proposal Distribution $g(x)$
Markov Chain Monte Carlo
- MCMC: Metropolis Algorithm (Sampling)
- Pseudocode
- MCMC: Bayesian Estimation

Bayesian Inference - Frequentism vs. Bayesianism

통계를 처음 공부하면 베이즈 추론이란 것은 그냥 계산식에 때려넣고 확률을 계산하는 식으로 배우지만, 역사적으로 보면 확률에 대한 새로운 paradigm 을 제시한 수학자의 유산이다. 우리가 익숙한 ‘통계’ 에선 동전을 던졌을 때 뒷면이 나올 확률은 0.5 라고 배운다. 하지만 토마스 베이즈가 정의한 베이지안 추론에선 확률을 완전히 새로운 관점에서 접근하며, 동전의 뒷면이 나올 확률을 0.5 라고 해석하지 않고 동전을 던졌을 시 ‘뒷면이 나왔다는 주장의 신뢰도가 0.5다’ 라고 해석한다.

전자가 Frequentism (빈도주의)며 후자가 Bayesianism (베이지안주의) 다.

빈도주의에선 어떠한 태스크를 무한히 수행했을 때 확률이 특정 값으로 수렴하며, 우린 이걸 해석하기 쉽게 ‘확률’ 이라고 부르지만, 베이지안주의에선 확률을 주장에 대한 신뢰도 로 해석하는 새로운 관점을 제시한다.

Bayesianism 은 베이즈가 베이즈 정리를 발표하면서 처음 나오게 된 통계를 재해석하는 관점이다.

\[P(H|E) = \frac{P(E \mid H)P(H)}{P(E)}\]

위 공식은 공학도에겐 익숙한 베이즈 정리의 공식이다. 베이즈 정리는 사전확률과 사후확률로 나뉘는데,

사전확률 (Hypothesis) = $P(H)$
사후확률 (Hypothesis given Evidence) = $P(H \mid E)$
우도 (Likelihood, Evidence given Hypothesis) = $P(E \mid H)$
새로운 정보의 신뢰도 (Evidence)= $P(E)$

이다. 베이즈 정리가 말하는 것은 가설 ($Hypothesis$), 혹은 어떤 사건이 발생했다는 주장이 있으면 새로운 증거($Evidence$) 를 통해 이 가설의 신뢰도 를 갱신해 내가는 과정이다.

Example: 이종현은 똑똑하다 라는 Statement 가 있다고 생각하자. 이 Statment 는 가설이 되며, 이 가설은 아무런 증거가 없으면 가설의 신뢰도는 처음 Statement 를 주장했을 때와 동일하다. 하지만 새로운 증거 (ex. 전공 평균평점이 4.3이다 ~~택도없다~~) 가 제시되면, 이 증거를 통해 ‘이종현은 똑똑하다’ 라는 가설의 신뢰도를 갱신해 나갈 수 있다.

베이즈 정리는 결국 추가적인 근거를 확보해 진리로 더 다가갈 수 있는 철학을 수학적으로 풀어낸 것이다.

Likelihood and Maximum Likelihood Estimation

MLE (Maximum Likelihood Estimation) 을 설명하기 전 다수가 헷갈려하는 통계적 단어를 짚고 넘어가보자. 모집단 ($Population$) 은 전체 집단이고, 모수($Parameter$) 는 모집단을 통계적으로 표현하는 수치들 (모평균, 모분산 등등) 이다.

명칭	설명
모집단 (Population)	특성의 전체 집단
모수 (Parameter)	모집단을 통계적으로 표현해주는 수치
표본집단 (Sample)	모집단에서 추출한 값들의 집합
통계치 (Statistics)	표본집단을 통계적으로 표현해주는 수치

표본집단 ($Sample$)은 모집단에서 랜덤하게 추출한 값들의 집합이다. 모수가 모집단을 통계적으로 표현한 수치면 표본집단은 통계치를 통해 표본집단을 표현한다.

실제 세상에선 모집단에 대한 모수를 알 수 없기 때문에, 모집단에서 표본집단을 추출 한 후 통계치를 통해 모집단에 대한 정보를 추정할 수 밖에 없다. 모집단에 대한 진리를 알기 위해 먼저 샘플링, 즉 표본집단을 추출하는 과정도 거쳐야 하고, 이 표본집단을 통해 모집단의 모수를 추정해야 한다.

$Sampling$ = 모집단 ($Population$) 에서 표본집단 ($Sample$) 을 추출하는 과정
$Parameter Estimation$ = 표본집단 ($Sample$) 을 통해 모집단 ($Population$) 의 모수 ($Parameter$) 을 추정하는 과정

통계학의 궁극적 목표는 모집단에 대한 완벽한 정보를 구축하는 것이지만, 앞서 언급한 것 처럼 사실상 불가능하다. 그렇기 때문에 일련의 과정을 걸쳐 모집단에 대한 지례짐작만 할 수 있는데, 얼마나 잘 지례짐작 하느냐가 관건이다. 그렇기 때문에 Sampling 과 Parameter Estimation 은 어떻게 하냐에 따라 결과가 상이 할 수 있는데, 최대우도법 (Maximum Likelihood Estimation) 은 Parameter Estimation 방법론 중 하나다. 최대우도법은 베이즈 정리의 Likelihood 라는 것을 이용하는데, 수식적으로 $P(E \mid H)$ 로 정의된다.

모집단에 대한 정보를 알기 위해 샘플링을 하고 파라미터를 추정한다.

파라미터를 잘 추정할 수 있다면 결국 그 모집단의 분포를 알게 되는것 - 통계적으로 유의미!

최대우도법은 베이즈 정리에서부터 파생된 것이기 때문에, 베이즈 정리의 우도공식인 $P(E \mid H)$ 보다 $P(D \mid {\theta})$ (Data given Parameter) 로 더 많이 표현한다. 베이지안 추론의 관점에서 포현하면, 데이터포인트가 이 파라미터에서 나왔다는 주장의 신뢰도다.

Sidenote: 여러 소스를 참고했는데, 사람들이 대부분 헷갈려하는 Likelihood, Likelihood Function, Total Likelihood 가 다 같은 말이다.

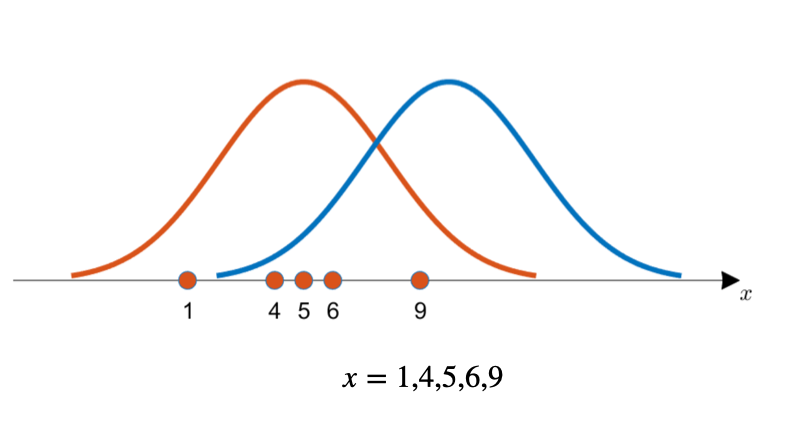
최대우도법을 예시로 설명해보겠다. 위의 모집단에서 샘플링한 4개의 데이터포인트가 있다. 이 데이터포인트들이 두개의 분포 중 어떤 모집단 분포에서 나왔을 가능성이 높은가를 정량적으로 계산하는 것이 Likelihood 이다. Likelihood 를 계산하려면 먼저 각 데이터포인트에 대한 Likelihood 기여도를 $P(x \mid \theta)$ 로 계산해야 한다.

모든 데이터포인트에 대한 Likelihood 기여도를 계산하고 곱해준 값이 바로 Likelihood (혹은 Total Likelihood, 혹은 Value of the Likelihood Function) 이 된다. 그리고 계산을 더 편하게 하기 위해 로그값을 취해 Log Likelihood 값으로 표현한다.

특정 데이터포인트에 대해 후보 파라미터를 주면, 이때 Likelihood 값이 제일 큰 파라미터를 선택해서 이 데이터포인트들이 이 파라미터를 갖는 모집단에서 나왔다고 가정하는 것이 최대우도법이다.

이때 파라미터를 추정한다 → 확률밀도함수를 추정한다 라는 것을 알 수 있다.

MLE: Parameter $\theta$ 로 구성된 $(\theta_1, ... ,\theta_m)$ 어떤 확률밀도함수 $P(x \mid \theta)$ 에서 관측된 표본 데이터집합을 $x (x_1, ... , x_n)$ 라고 했을 때, 이 표본들로부터 Parameter $\theta$ 를 추정하는 방법.

Values	Functions
Likelihood	$P(D\|\theta)\ or \ P(x\|\theta)$
Likelihood 기여도	$P(x_k\|\theta)$
Likelihood Function	$P(x\|\theta) = \prod P(x_k\|\theta)$
Log-Likelihood Function	$L(\theta\|x) = \sum logP(x_k\|\theta)$
Maximum Likelihood Estimation	$argmax \ L(\theta\|x)$

Rejection Sampling

최대우도법이 파라미터 추정방법이였다면 기각샘플링 (Rejection Sampling)은 말 그대로 샘플링 방법이다. 샘플링은 간단하게 보면 모집단에서 표본을 추출하는 것이지만, 모집단의 분포를 모르기 때문에 실제 모집단의 분포와 비슷하게 샘플링을 하는 것은 어렵다.

수학적인 관점에서 샘플링을 보면 cdf 의 역함수 연산을 하는 것인데, 이 프로세스 자체가 어려울 뿐만 아니라 애초에 확률밀도함수에 대해 적분연산을 취해줘야 cdf 를 구할 수 있기 때문에 수치적으로 정확하지도 않다.

즉, 설령 모집단의 확률밀도함수를 알고 있다고 해도 샘플링은 어렵다.

여기서 기각샘플링은 샘플들이 모집단의 확률밀도에 맞게 샘플링을 해주는 착한 알고리즘이다.

Proposal Distribution $g(x)$

기각샘플링을 이해하기 위해 제안분포 (Proposal distribution) 이란 것을 알아야 한다. 제안분포 $g(x)$ 는 명칭에서도 알 수 있듯이 수학자가 제안하는 분포다. 어떤 분포를 사용해도 좋지만, 타깃 분포와 유사한 분포, 혹은 샘플링을 쉽게 할 수 있는 분포를 사용하는게 일반적이다.

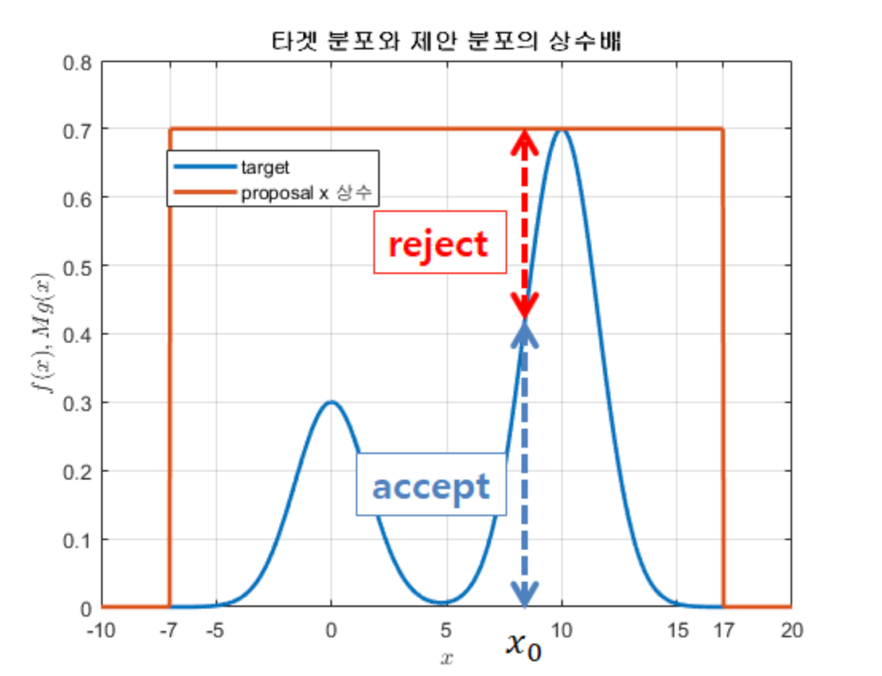
예시를 통해 설명해 보겠다. 위 그림을 참고하며 제안분포를 설정 후 타깃분포의 최고점을 감쌀 만큼 제안분포를 상수배 해주고 $(Mg(x))$, 제안 분포에서 랜덤한 값을 추출해서 해당 값과 해당 값에 대한 타깃분포의 값을 비교한다 (말이 헷갈리지만 그림에서 붉은 점선과 푸른 점선의 길이를 비교하는 것이다). 만약 타깃분포의 값이 더 크면 해당 샘플을 수용한다.

여기서 두개의 값들을 비교하는 것은 결국 랜덤값에 대한 두 분포의 Likelihood 를 비교하는 것이다.

Likelihood: $P(x \mid \theta)$, or the probability of x in a given distribution.

이런 식으로 모든 데이터포인트에 대해 기각샘플링 알고리즘을 사용하면, 타깃 분포를 따르는 샘플들을 추출 할 수 있다. 기각샘플링은 효과적인 알고리즘이지만, 단점은 기각되는 데이터 포인트가 많기때문에 Computational Complexity 가 크다는 것이다. 이를 극복하기 위해 나온 알고리즘이 바로 해당 포스팅의 주제인 $Markov \ Chain \ Monte \ Carlo \ Algorithm$ 이다 ~~빌드업~~.

Markov Chain Monte Carlo

Markov Chain: $t-1$ 상태에서 $t$ 로 넘어갈 때, $t$ 가 $t-1$ 으로부터만 직접적인 영향을 받는 프로세스를 Markov Chain 이라 한다.

Monte Carlo: 무한한 계산으로만 정답을 알 수 있는 것을 유한한 시도만으로 통계적 정답을 추정하기 위한 시뮬레이션.

이 두가지 아이디어를 합친 것이 MCMC 인데, 간단하게 생각하면 최대우도법과 기각샘플링 같은 파라미터 추정법과 샘플링 방식을 하나로 합친 알고리즘이다.

MCMC 는 이전에 언급한 베이지안 추론, 최대우도법, 그리고 기각샘플링에 기초하고 있고, MCMC는 다량의 세분화된 알고리즘이 있지만 동일한 pseudo-process 를 따른다.

MCMC Pseudo-Process

Random Initialization

제안분포를 이용해 첫 sample 기반 다음 sample 을 추천 (Markov Chain 부분)

특정 기준에 다라 추천된 sample 을 Accept/Reject

Repeat.

MCMC - Metropolis Algorithm (Sampling)

MCMC 알고리즘 중 가장 유명한 소분류 알고리즘인 Metropolis Algorithm 을 예시로 설명하겠다. 해당 그림에 그려진 유사확률밀도함수를 우리의 타깃 분포라고 가정하자.

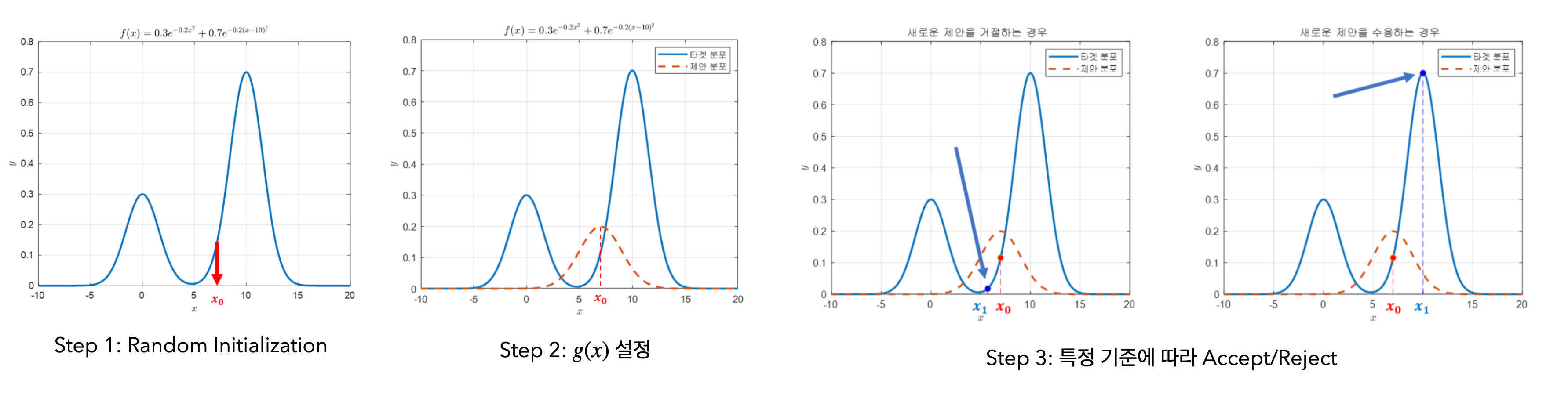
먼저 랜덤한 초기값을 고르고 $x_0$ 이라 설정한다.

$x_0$ 을 평균으로 갖는 제안분포 $g(x)$ 를 설정한다. 이때 제안분포를 기각샘플링처럼 마음대로 정할 수 있지만, 예시로 설명하는 이 알고리즘은 제안분포를 대칭분포로 사용하는 Metropolis-Hastings 알고리즘이다.

초기값 $x_0$ 을 기준으로 제안분포를 설정 한 뒤, 해당 제안분포에서도 랜덤한 샘플 $x_1$ 을 추출한다. 타깃분포에 대한 이 두 샘플의 Likelihood 를 계산 한 뒤, $x_1$ 의 Likelihood 가 $x_0$ 보다 높다면 $x_1$ 을 샘플로 Accept 한다.

$x_1$ 을 다시 $x_0$ 로 설정한 뒤 반복한다.

MCMC 의 과정을 보면 기각샘플링과 굉장히 유사하다. 하지만 차이점은 기각샘플링은 하나의 샘플에 대해서 타깃분포와 제안분포의 Likelihood 를 비교하는 반면, MCMC 샘플링에선 제안분포를 통해 다음 샘플을 추천받아 이전 샘플과 다음 샘플의 Likelihood 를 비교한다. 여기서 다음 샘플이 이전 샘플에 따라 추출이 되기 때문에 Markov Chain 이란 이름이 붙은 것이다.

여기서 약간 의문점이 들 수도 있는게, 샘플을 기각하다 보면 샘플링 되는 값들은 타깃분포의 한 optima 로 수렴할 것이다. 이를 방지하기 위해 MCMC 에선 일종의 패자부활전 을 진행한다.

기준	function
Accept	$\frac {f(x_1)}{f(x_0)}>1 \ or > u$
Reject	$\frac {f(x_1)}{f(x_0)}<1 \ and < u$

만약 $x_0, x_1$ 두 샘플의 Likelihood를 나눈 값이 1을 넘지 못한다면 ($x_1$ 의 Likelihood 가 $x_0$보다 작다면) $x_1$ 을 바로 reject 하는 것이 아니고 uniform distribution 을 이용해서 MCMC 의 프로세스를 한번 더 수행한다. Uniform dist. 에서 랜덤한 값 $u$ 를 추출하고, 만약 $x_0, x_1$ 에 대한 Likelihood 를 나눈 값이 이 랜덤한 값 $u$ 보다 크면 $x_1$ 을 Accept 한다.

$x_0, x_1$ 에 대한 Likelihood 를 나눈 값이 이 랜덤한 값 $u$ 보다 작으면 $x_1$ 을 reject 하지만, 샘플링이 되지 않을 뿐 $x_1$ 은 버려지지 않고 새로운 제안분포를 설정하기 위해 $x_0$ 값으로 update 된다.

정리를 하자면 두 샘플값에 대한 Likelihood 를 비교한 값이 1 혹은 $u$ 보다 크면 그 샘플을 Accept 하고, 1 혹은 $u$ 보다 작으면 그 샘플을 Reject 한다.

Pseudocode

Initialize $x_0$

for $i = 0$ to $N-1$

Sample $u \sim U_{[0,1]}$

Sample $x_{new} \ g(x_{new} \mid x_i)$

if $u < A(x_i,x_{new} = min(1, \frac {f(x_{new})}{f_(x_i)}))$

$x_{i+1} = x_{new}$

else

$x_{i+1} = x_i$

지금까지 예시로 설명한 알고리즘은 MCMC 의 Metropolis 알고리즘으로, 제안분포를 대칭분포로 설정하고 진행하는 알고리즘이다. 만약 기각샘플링에서 잠깐 언급한 것 처럼 타깃분포와 유사한 분포로 제안분포를 설정하고 싶다면 Metropolis 알고리즘을 조금 변형한 Metropolis-Hastings 알고리즘을 사용하면 된다.

MCMC - Bayesian Estimation Algorithm

MCMC Metropolis 가 기각샘플링 같은 샘플링 방법이라면, 지금 살펴볼 MCMC Bayesian Estimation 은 최대우도법과 같은 파라미터 추정 알고리즘이다.

최대우도법과 MCMC Bayesian Estimation 의 차이는 최대우도법에선 모든 $x$에 대해 Likelihood 를 점검하지만, MCMC Bayesian Estimation 에선 제안분포를 통해 관찰하고자 하는 파라미터값을 제안받아서 점검한다.

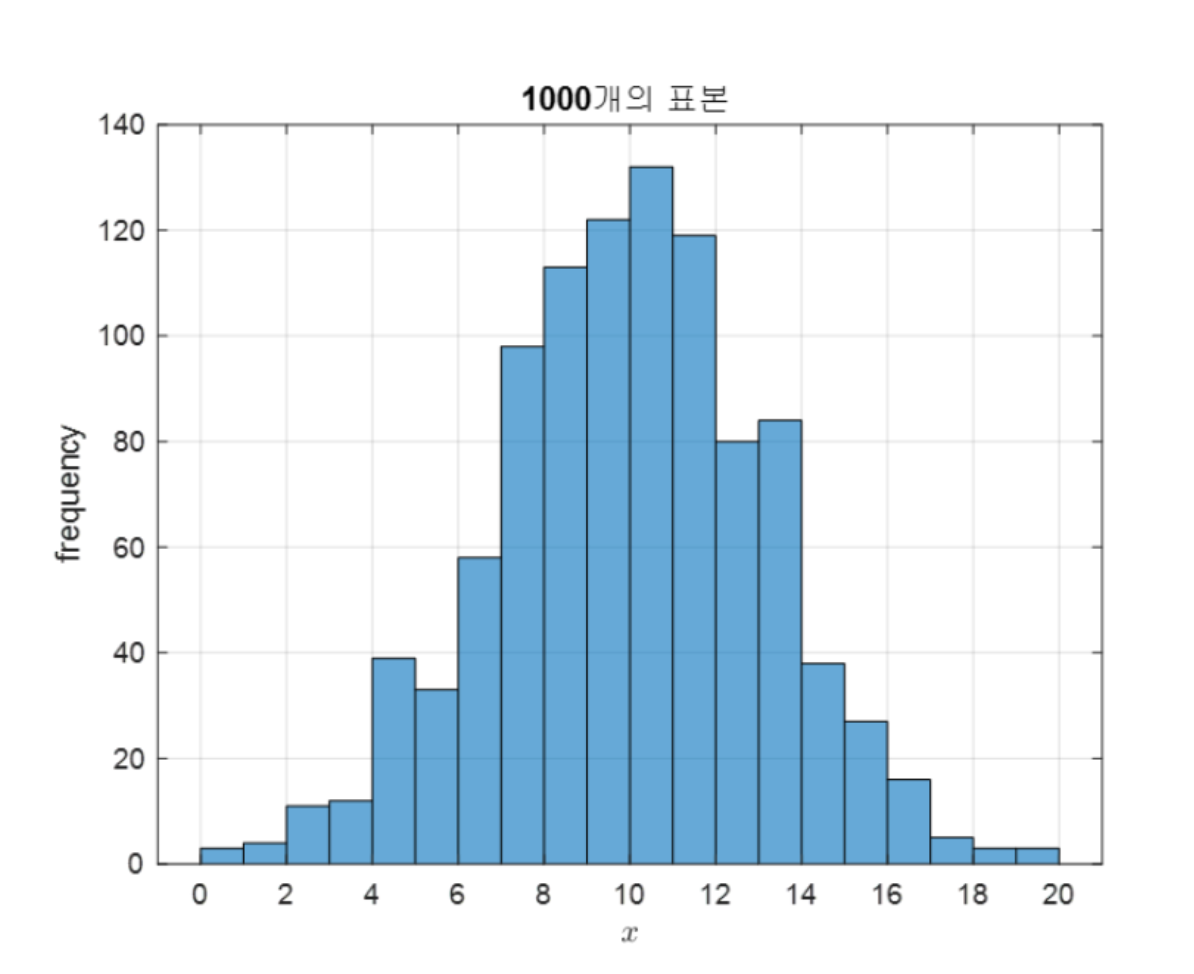
동일하게 예시로 설명을 해보겠다. 여기 총 population 이 3만인 모집단에서 샘플링한 표본집단의 분포가 있다. 이 분포를 통해 모집단의 파라미터인 평균을 추정하려면 MCMC Bayesian Estimation 을 사용하면 된다.

MCMC Metropolis 와 동일하게 먼저 랜덤한 파라미터값 $\theta$ 를 초기화한다.

이 랜덤한 파라미터값을 기준으로 제안분포를 설정하고, 이 제안분포로 새로운 파라미터 값을 추천받는다.

이 두 파라미터 값에 대한 타깃분포를 비교할 때, $f_{new}(x)/f_{old}(x) > 1$ 이면 해당 파라미터를 Accept 한다.

여기서 샘플링 알고리즘과의 차이점은 타깃함수의 파라미터가 변경된 경우를 비교하는것이다. 파라미터가 변경된다는 것은 타깃분포 자체가 동적으로 바뀐다는 것인데, 샘플링 알고리즘에선 타깃분포는 변하지 않는다.

Accept 되는 기준식을 풀어서 써보면 처음에 등장한 베이즈 정리로 값을 구할 수 있다. 파라미터의 타깃분포에 대한 확률은 $P(\theta \mid Data)$ 로 쓸 수 있고, 이것이 사후확률이라면 베이즈 정리를 통해 사전확률에 대한 공식으로 풀어낼 수 있다.

결국 MCMC Bayesian Estimation 에서 $\theta$ 가 Accept 되는 기준은 베이즈 정리를 통한 Likelihood * Prior 값이 되는것을 알 수 있다.

\[\frac{f_{new}(x)}{f_{old}(x)} > 1\] \[\frac{P(\theta = \theta_{new} \mid Data)}{P(\theta = \theta_{old} \mid Data)}>1\] \[\frac{f(D \mid \theta=\theta_{new})P(\theta=\theta_{new})/f(D)} {f(D \mid \theta=\theta_{old})P(\theta=\theta_{old})/f(D)}>1\] \[\frac{f(D \mid \theta=\theta_{new})P(\theta=\theta_{new})} {f(D \mid \theta=\theta_{old})P(\theta=\theta_{old})}>1\] \[f(D \mid \theta) = \prod_{i=1}^N f(d_i \mid \theta)\]
$\frac{f(D \mid \theta=\theta_{new})P(\theta=\theta_{new})} {f(D \mid \theta=\theta_{old})P(\theta=\theta_{old})}>1$

$\frac{f(D \mid \theta=\theta_{new})P(\theta=\theta_{new})} {f(D \mid \theta=\theta_{old})P(\theta=\theta_{old})}>1$
\[\prod_{i=1}^{N}\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(d_i-\mu)^2}{2\sigma^2}\right)\] \[\sum_{i=1}^{N}\left\lbrace\log\left(\frac{1}{\sigma\sqrt{2\pi}}\right)-\frac{(d_i-\mu)^2}{2\sigma^2}\right\rbrace\] \[\sum_{i=1}^{N}\left\lbrace-\log(\sigma\sqrt{2\pi})-\frac{(d_i-\mu)^2}{2\sigma^2}\right\rbrace\]
$\frac{\sum_{i=1}^{N}\left\lbrace-\log(\sigma\sqrt{2\pi})-\frac{(d_i-\mu_{new})^2}{2\sigma^2}\right\rbrace + \log(P(\mu = \mu_{new}))} {\sum_{i=1}^{N}\left\lbrace-\log(\sigma\sqrt{2\pi})-\frac{(d_i-\mu_{old})^2}{2\sigma^2}\right\rbrace + \log(P(\mu = \mu_{old}))} > 1$

Contents