Logistic Regression
Contents
- Logistic Regression
- Odds and the Logit Function
- Learning and Maximum Likelihood Estimation
해당 포스트는 2021년 1학기 고려대학교 강필성 교수님의 ‘다변량분석’ 강의를 참고하여 작성되었습니다.
이미지는 강필성 교수님의 강의 슬라이드에서 발췌하였습니다.
A+ 감사했습니다 교수님
Logistic Regression
로지스틱 회귀분석은 전 장에서 살펴본 다중선형회귀분석을 차용한 모델이다. 다중선형회귀분석의 종속변수의 범위는 연속적인 실수값이지만, 로지스틱 회귀분석은 종속변수가 binary 하다.
다중선형회귀분석의 식을 그대로 binary \(\hat y\) 값을 추정하는데 사용한다면 한가지 문제가 생긴다. 우변은 연속적인 값을 표현하는데 사용되지만, 좌변은 binary 하기 때문에 구한 회귀식의 범위가 종속변수의 범위를 벗어난다. 그렇기 때문에 로지스틱 회귀분석은 약간의 수학적 트릭을 사용해서 다중선형회귀분석의 우변의 꼴을 유지하면서 binary 종속변수를 표현할 수 있게 한다.
로지스틱 회귀분석에서 ‘회귀식’의 꼴을 유지하는데 있어 몇가지 장점이 있다.
- 추정된 \(\hat \beta\) 값을 통해 설명변수의 유의미도를 파악할 수 있다.
- 해당 설명변수를 통해 최종 확률이 증가하는지/감소하는지 파악할 수 있다.
회귀식의 꼴을 유지하면 위와 같이 모델의 설명력을 그대로 유지할 수 있다는 장점이 있다. 그렇기 때문에 로지스틱 회귀분석은 y 에 대한 ‘logit’ 함수를 통해 설명변수와의 선형결합을 표현 할 수 있다.
Odds and the Logit Function
로지스틱 회귀분석을 알기 위해 먼저 Odds (승산) 의 개념을 익혀야 한다. 승산은 스포츠 중계에서 흔하게 볼 수 있는 수치로, ‘‘해당 팀의 승산이 몇대몇 (ex. 9:2) 이다’ 로 표현된다.
예시를 들어보자. 2010년 월드컵에서 전문가들은 스페인의 ‘승산’이 9:2 라고 산출했다. 이를 승산식에 넣으면 p, 즉 우승 확률을 구할 수 있다.
\[Odds = {p \over 1-p} = {2 \over 9} \\ 9p = 2-2p \\ p = {2 \over 11}\]로지스틱 회귀분석은 바로 이 승산을 도입해서 binary 값을 연속형으로 표현하는데 사용한다.
| Equation | Explanation |
|---|---|
| \(y \in \{0,1\}\) | 기존 종속변수는 binary 값이다. |
| \(P(y=1) \in [0,1]\) | 종속변수가 1일 확률을 종속변수로 지정하여 0과 1 사이 연속적인 값으로 표현한다. |
| \(p = P(y=1)\) | 종속변수가 1일 확률을 Odds 의 p 로 치환한다. |
| \(0 \leq {p \over 1-p} \leq \infty\) | 종속변수의 값의 범위가 0부터 \(\infty\) 로 변한다. |
| \(-\infty \leq ln{p \over 1-p} \leq \infty\) | Odds 에 로그를 씌워 범위를 실수로 확장한다. |
먼저 종속변수의 binary 값 중 1일 확률을 Odds 와 비교하면 아래의 그래프와 같다.
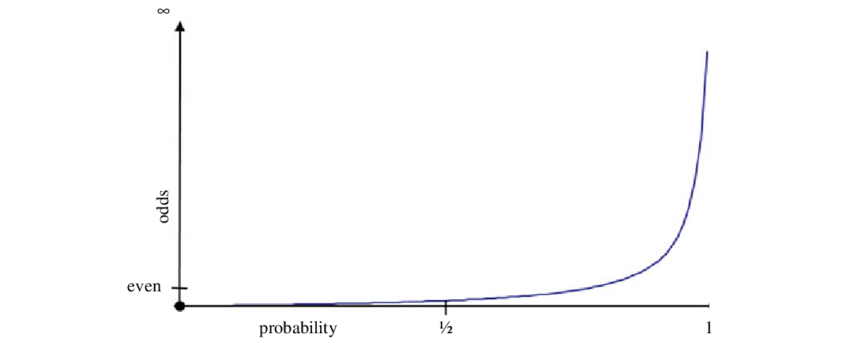
종속변수를 Odds 로 설정하면 범위가 0부터 무한대로 늘어난다. Even 이라고 되어있는 지점은 P(y=1) = 0.5 이고, 대응하는 Odds 값은 1이다. 하지만 Odds 는 비대칭이고 \(-\infty\) 를 표현하지 못하기 때문에, 로그함수를 씌워준다.
\[p=0 \rightarrow Odds \rightarrow 0 \rightarrow ln \rightarrow -\infty \\ p=1 \rightarrow Odds \rightarrow \infty \rightarrow ln \rightarrow \infty\]위와 같이 0과 1 사이의 확률을 승산의 로그함수에 대입하니 범위가 모든 실수로 확장되는 것을 볼 수 있다. 이를 logit function 이라 한다.
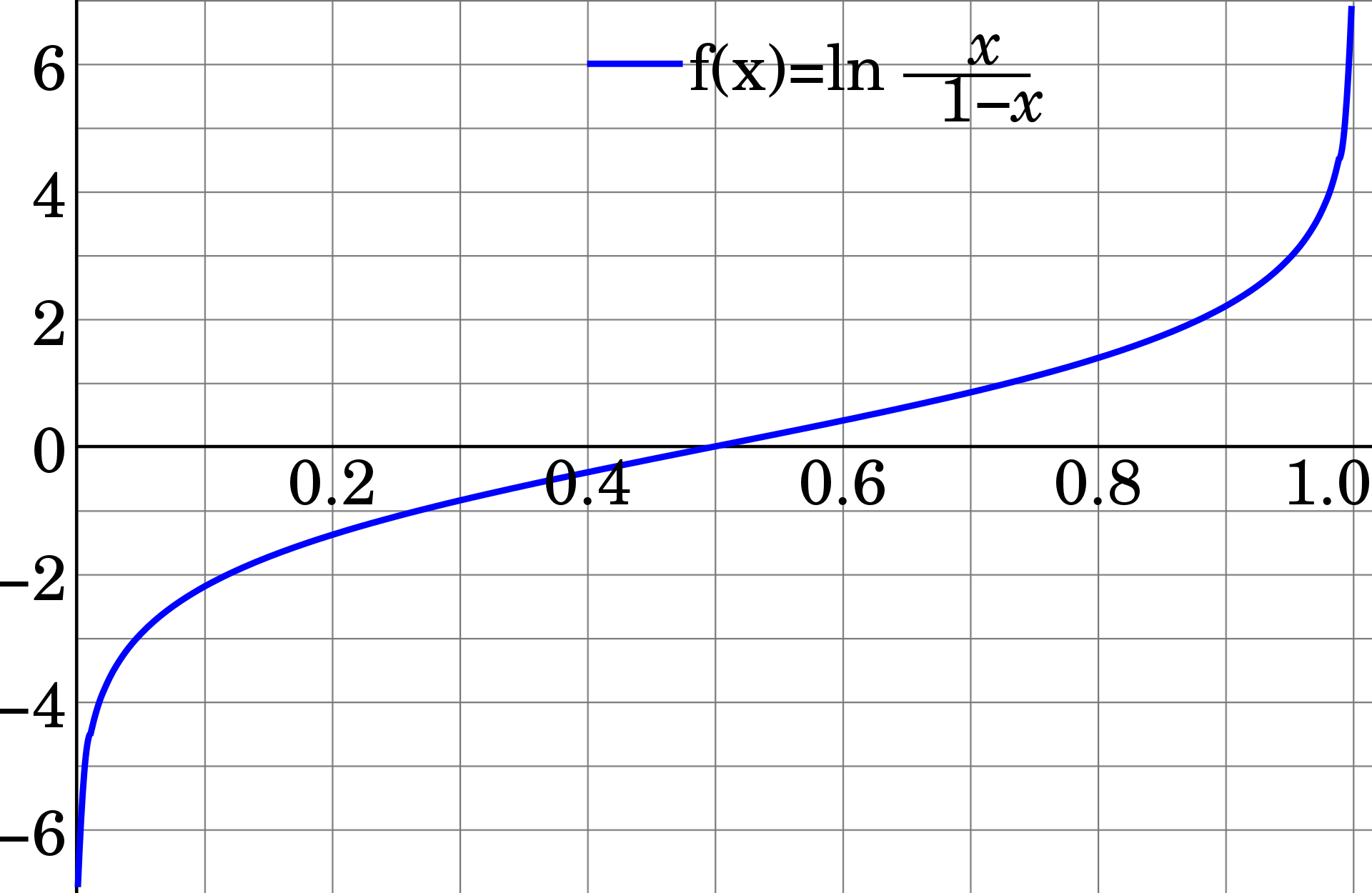
즉, 회귀식의 우변의 꼴을 유지하면서 binary 한 종속변수를 표현 할 수 있게 된 것이다.
\[ln(Odds) = ln({p \over 1-p}) = \hat \beta_0 + \hat \beta_1x_1 + \hat \beta_2x_2+...+\hat \beta_dx_d\]위 식은 성공확률에 대한 로그승산을 선형식으로 추정한 것이다. 하지만 회귀식을 추정하는 이유는 새로운 데이터포인트가 들어오면 이에 대한 정의한 확률 \(P(y=1)\) 을 알고 싶은 것이기 때문에, 위의 회귀식을 p 에 대해서 정리해야 한다.
\[{p \over 1-p} = e^{\hat \beta_0 + \hat \beta_1x_1 + \hat \beta_2x_2+...+\hat \beta_dx_d} \\ p = {1 \over 1+e^{-\hat \beta_0 + \hat \beta_1x_1 + \hat \beta_2x_2+...+\hat \beta_dx_d}} \\ \sigma(x|\beta)\]위 식으로 새로운 데이터포인트가 들어오면 정의한 1범주에 속할 확률을 구할 수 있다. 자세히 보면 \(\hat\beta_0\) 상수가 0이고 1차원의 설명변수의 계수가 1이면 식은 Sigmoid Function 이 된다. 확률에 대한 해당 식은 \(\sigma (x \mid \beta)\) 라고 표현하기도 하고, 실제 그래프상 그려지는 함수다.
Learning and Maximum Likelihood Estimation
앞서 살펴본 다중선형회귀분석은 closed form solution 이 존재하는 몇 안되는 알고리즘 중 하나다. \(\hat \beta = (X^TX)^{-1}X^TY\) 의 행렬연산을 통해 명시적 \(\hat \beta\) 의 값을 구할 수 있지만, 로지스틱 회귀분석은 그렇지 않다. 로지스틱 회귀분석은 학습과정에서 항상 다른 모델이 학습되기 때문에, 이 과정을 살펴보고자 한다.
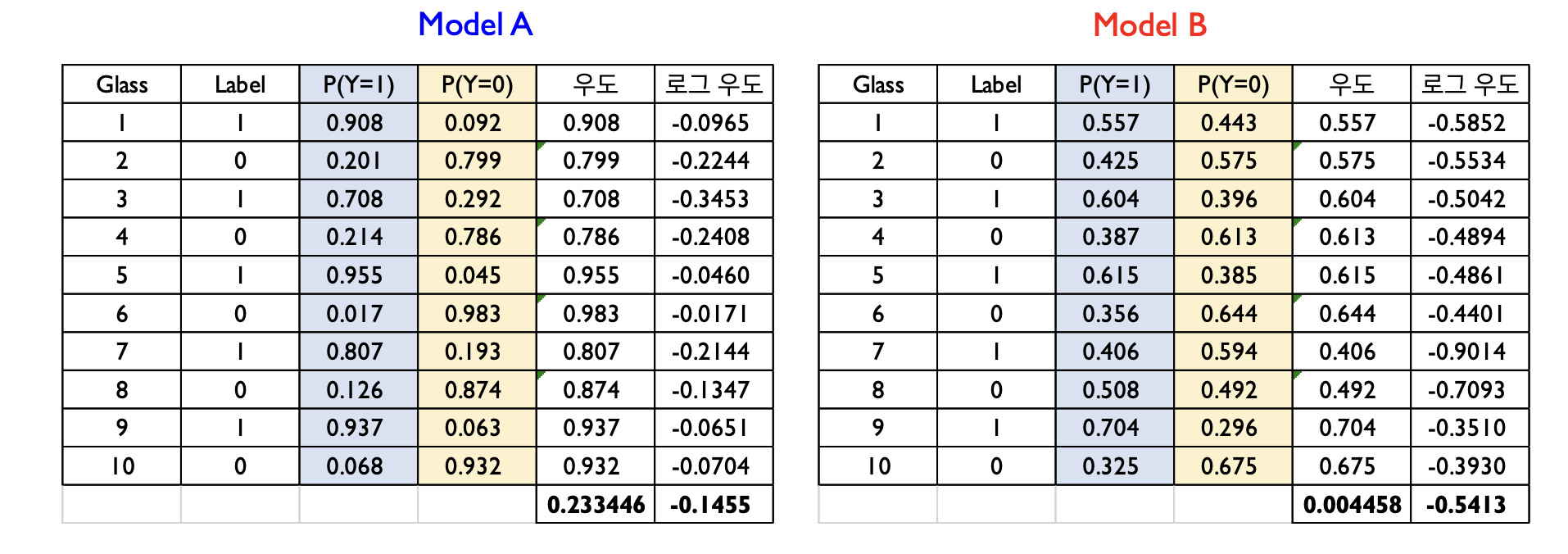
위에 같은 데이터셋으로 학습된 두개의 로지스틱 회귀분석 모델이 있다. Label 1 은 불량제품이며, Label 0 은 정상제품이다. 이 두개의 모델 중 더 나은 모델을 고르자면 모델 A다. 모델 A와 B 모두 정답 Label 에 더 높은 확률을 부여했지만 (맞게 예측했지만), 모델 A 는 정답범주에 속할 확률을 더 높게 산출하고 있기 때문에 더 나은 모델이라고 할 수 있다.
이를 우도(Likelihood) 라고 하며, 베이즈 정리에서 등장하는 \(P(Evidence \mid Hypothesis)\) 다. 만약 데이터셋의 모든 샘플들이 독립적으로 생성되었다고 가정하면 (iid assumption), 데이터셋에 대한 전체 우도는 모든 샘플의 우도의 곱으로 계산된다.
\[if \ A \cap B = \varnothing, \\ P(AB) = P(A)P(B)\]그렇기 때문에 같은 데이터셋을 통해 생성된 두개의 로지스틱 회귀분석 모델을 비교할 시, 데이터셋의 우도를 통해 어떤 모델이 더 나은지 비교할 수 있다. 하지만 우도는 각 샘플의 우도의 곱으로 계산되기 때문에, 실제 데이터셋의 샘플크기가 많아질수록 0에 수렴한다. 이를 방지하기 위해 로그를 씌운다.
우도를 통해 모델의 성능을 비교할 수 있지만, 반대로 생각해보면 이를 cost function 으로 사용해 모델을 학습시킬 수도 있다. 이를 MLE (Maximum Likelihood Estimation) 이라 하며, 우도를 최대화 시키는 \(\hat \beta\) 값을 찾도록 학습시키는 것이다.
\[P(\textbf{x}_i,y_i|\beta) =\sigma(\textbf{x}_i|\beta)^{y_i}(1-\sigma(\textbf{x}_i|\beta))^{1-y_i}\]각 샘플의 우도를 구하는 식은 위와 같다. Integer programming 에서 사용되는 트릭과 비슷하게 \(y_i\) 가 1일때 우변의 앞부분이 활성화되고, \(y_i\) 가 0이면 뒷부분이 활성화되도록 formulating 한 것이다. 이때 앞서 언급한 것 처럼 \(\sigma(X_i \mid \beta)\) 는 \(p = {1 \over 1+e^{-\hat \beta_0 + \hat \beta_1x_1 + \hat \beta_2x_2+...+\hat \beta_dx_d}}\) 이다. 즉, 해당 샘플의 Label 이 타깃 Label (\(y_i=1\)) 이면 확률을 구하고, 타깃 Label 이 아니면 1에서 확률을 뺀 것으로 해당 샘플의 우도를 구할 수 있다. 각 샘플의 우도를 구하는 식으로 데이터셋의 우도를 구하는 식은 다음과 같다.
\[L(\textbf{X},\textbf{y}|\beta) = \prod^N_{i=1} P(\textbf{x}_i,y_i|\beta) = \prod^N_{i=1}\sigma(\textbf{x}_i|\beta)^{y_i}(1-\sigma(\textbf{x}_i|\beta))^{1-y_i}\]앞서 언급한 것 처럼 데이터셋의 우도는 iid 가정 하에 모든 샘플의 우도의 곱이다.
\[logL(\textbf{X},\textbf{y}|\beta) = \sum y_i log\sigma(\textbf{x}_i|\beta)+(1-y_i)log(1-\sigma(\textbf{x}_i|\beta))\]양변에 로그를 취해주면 product 는 summation 이 되므로 위의 식이 된다. 위 식으로 데이터셋의 우도를 최대화 시키는 \(\hat \beta\) 를 구하는 것이 MLE 다. MLE 를 loss function 으로 사용 할 경우 Gradient Descent 를 사용하는 경우가 많다.
최종적으로 우도를 최대화 시키는 회귀식을 구하면, 새로운 샘플에 대해 해당 샘플이 타깃 Class 에 속해있을 확률을 구할 수 있다. 하지만 로지스틱 회귀분석의 목적은 결과적으로 binary classification 이기 때문에, Cutoff 를 정해야 한다. 즉, 어느정도의 확률 이상만 타깃 Class 라고 분류해주는 Cutoff 를 설정해야 한다. 가장 많이 사용되는 cutoff 는 직관적이게 0.5 다. 하지만 실제 상황에선 특정 구간 내 설명변수와 종속변수는 정비례하지만 구간을 벗어나면 설명변수가 확률에 영향을 끼치는 정도가 작아진다. 그렇기 때문에 해당 데이터셋이 만들어진 상황과 목적에 따라 cutoff 를 설정해야 한다. 예시로 불량을 잡아내는게 매우 중요한 QC 같은 분야에선 타깃 Class 가 1이면, cutoff 를 매우 낮게 잡아 (ex. 0.2) 아주 작은 확률도 불량이라고 정하는게 중요하다.