Dimensionality Reduction - Isomap (Isometric Feature Mapping)
Contents
- Isometric Feature Mapping (Isomap)
- Step 1: Construct Neighborhood graph
- Step 2: Compute the Shortest Path
- Step 3: Construct \(d\) - dimensional Embedding with MDS
Isometric Feature Mapping (Isomap)
대표적인 선형변환 차원축소 방법론엔 PCA (주성분분석) 와 MDS (다차원척도법) 가 있다면, 대표적인 비선형변환 차원축소 방법론엔 Isomap 과 LLE 가 있다. 두 방법론은 같은 연도의 같은 Journal 의 같은 권호수에 출판되었으며, 위상수학의 manifold 를 머신러닝에 접목시킨 manifold learning 의 주역이 되기도 했다. 두 방법론 중 Isomap 에 대해 먼저 알아보자.
선형변환 차원축소 방법론 (PCA, MDS) 는 computational complexity 가 낮고 전역최적해를 보장해준다는 장점이 있지만, 데이터가 애초에 선형성을 띄고 있지 않는다면 결과가 좋지 못하다는 단점이 있다.
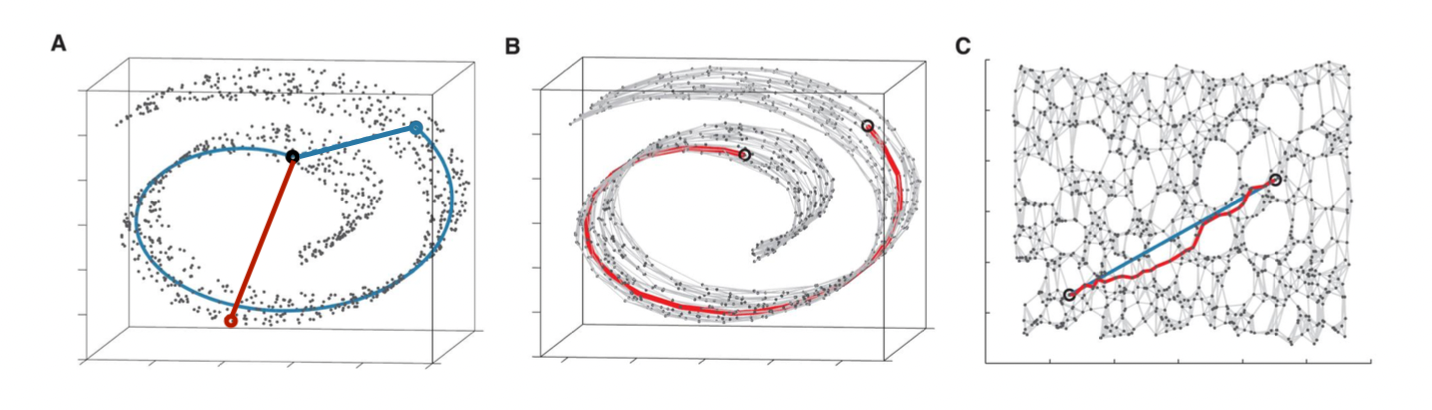
위 이미지의 그림 A 를 보자. 데이터는 3차원의 공간에 있으며, 2차원의 직사각형을 돌돌 만 Roll 형태를 띄고 있다. 해당 데이터에 MDS 를 적용하여 거리에 대한 정보를 보존하며 낮은 차원으로 차원축소를 했다고 가정하자. 이때 검은 점과 푸른 점은 실제 3차원 공간에서도 꽤나 가깝기 때문에, euclidean distance 를 proximity measure 로 정의한 MDS 상 아무런 문제가 되지 않는다. 하지만 이런식으로 차원축소를 한다면 intrinsic dimension 의 정보가 사라진다는 치명적인 단점이 있다.
Intrinsic dimension 이란 데이터가 위치한 내재적인 차원을 의미하고, intrinsic dimension 을 펼친 공간을 manifold 라고 한다. 검은 점을 기준으로 푸른 점과의 euclidean 거리는 붉은 점보다 가깝지만, 실제 manifold 상 거리를 어림짐작한다면 푸른 점은 훨씬 멀리 떨어져 있다. 그렇기에 Isomap 의 핵심 아이디어는 보존하고자 하는 거리 정보를 Intrinsic manifold 상의 거리로 정의하여 차원축소를 진행하는 것이다.
두번째 그림 B 는 객체를 node 로 취급하고 이웃들끼리 edge 를 그려 그래프 구조를 통해 intrinsic manifold 의 구조를 최대한 보존한 것이다. Intrinsic manifold 상 두 객체간의 거리를 알고싶다면 그려진 그래프를 따라 최단 경로로 이동하면 된다. 그림 C 를 보면 manifold 를 펼쳐놓은 것인데, 이때 manifold 상 실제 최단거리는 푸른색 직선이고, 이를 최대한 비슷하게 따라간 길이 붉은색으로 표시된 그래프를 통해 따라간 길이다.
| Proximity Measure | |
|---|---|
| MDS | Original Space 의 최단거리 (Euclidean, Manhattan) 혹은 유사도 (Cosine, Jaccard) |
| Isomap | Intrinsic Manifold 속 그래프 상 최단거리 |
Intrinsic Manifold 의 개념을 이해했다면 Isomap 은 굉장히 단순해진다.
Step 1: Construct Neighborhood graph
Manifold 상 거리를 표현하기 위해 객체들을 연결해주는 그래프를 구해야 한다. 이때 하나의 점을 이웃들과 연결시키는 방법은 크게 두가지다.
Epsilon Neighborhood
DBSCAN 에서도 clustering 으로 사용하는 epsilon neighborhood 는 정의해둔 radius \(\epsilon\) 안에 존재하는 점들을 모두 연결시키는 방법론이다.
K-Nearest Neighbor
K-NN 은 한 점에서 가장 가까운 \(k\) 개의 점을 연결시키는 방법론이다.
두개의 방법론 모두 타당하지만, 결국 임의의 두 객체간의 거리를 전부 계산해야 하기 때문에 객체 단 하나라도 path 가 끊겨있으면 안된다. 그렇기에 일반적으론 K-NN 이 사용되지만 K-NN 또한 ‘short circuit errors’ 의 문제가 있다. Short circuit errors 란 \(k\) 가 너무 커 실제 manifold 의 정보보다 과하게 객체들을 연결시키는 에러다.
Step 2: Compute the Shortest Path
모든 점들이 연결되었다면 모든 객체들에 대한 graph 상 서로간의 거리를 계산해야 한다. 이때 각 객체는 기존 차원에서 euclidean distance 로 그래프가 연결 되어있기 때문에, 알고리즘 수업에서 배운 그 어떤 최단거리 알고리즘을 사용할 수 있다. 대표적으론 Dijkstra Algorithm, Bellman-Ford Algorithm, Floyd-Warshall Algorithm 이 있다.
개인적으론 다익스트라 알고리즘을 좋아한다. 비교적 낮은 time complexity 를 갖기도 하고, 처음 배웠을 때 이름이 \(D_{ijk}\)stra (\(i,j,k\) 간의 \(Distance\)) 로 보였기 때문이다. 에르허츠 다익스트라의 어록들도 한몫한다.
“The question of whether a computer can think is no more interesting than the question of whether a submarine can swim.” - Edsger W. Dijkstra
Step 3: Construct \(d\) - dimensional Embedding with MDS
그래프를 구축하고 각 객체간의 그래프상 최단거리를 Proximity matrix \(\mathbf{D}\) 로 정의한 뒤, 기본적인 Multi-Dimensional Scaling 을 진행하면 된다. 즉, Isomap 은 객체간 거리를 intrinsic manifold 상의 거리로 정의한 것 뿐이지, 저차원으로 embedding 하는 과정은 MDS 와 다름없다. 하지만 intrinsic manifold 로 거리를 정의했기 때문에, 본질적인 거리정보가 traditional MDS 보다 많이 보존된다.
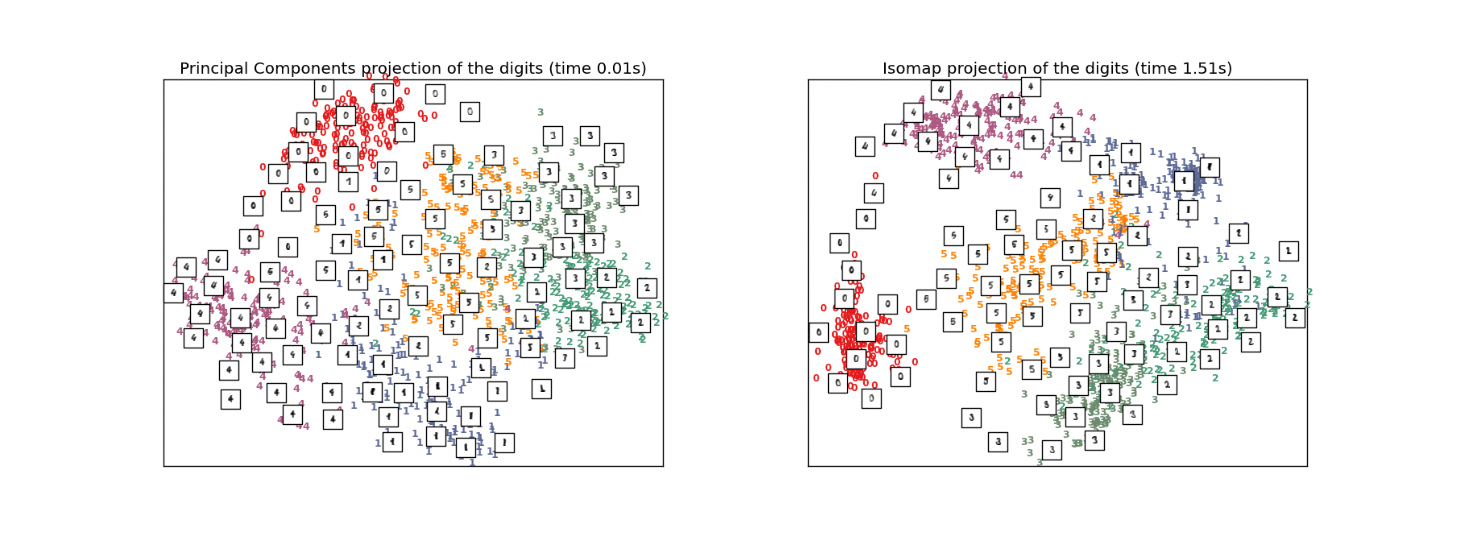
위 예시는 선형변환 차원축소방법론인 PCA 와 Isomap 의 결과의 시각화이다. 궁극적인 task 가 classification 이라면 Isomap 이 우월한 방법론인 것을 알 수 있다.
해당 포스트는 강필성 교수님의 Business Analytics 를 참고하여 작성되었습니다.