Generative Adversarial Networks (Goodfellow et al. 2014)
Contents
- Introduction
- Generative Models
-
Objective function of GAN
- Discriminator’s Perspective: Maximize
- Generator’s Perspective: Minimize
- Global Optimality
Introduction
GAN 은 Goodfellow 와 Bengio 등 저명한 딥러닝 연구자들이 2014년 처음 고안한 후, 딥러닝에 대한 대중의 이목을 크게 끈 새로운 생성 모델이다. 굉장히 단순하면서도 아름다운 목적함수를 통해 딥러닝의 capability 에 대한 새로운 패러다임을 제시했으며, 반대로 실전에서 학습시키기 굉장히 어려운 모델로 악명이 높기도 하다. GAN 은 2022년 현재 폭발적인 연구와 함께 고도성장했으며, This Person Does Not Exist 와 같은 일반인이 구분하기 불가능할 정도로 사실적인 샘플을 생성할 수 있다. StyleGAN, SinGAN, BEGAN, DCGAN 등 특정 분야에서 고도화 된 모델들은 논문이 나오는 속도를 따라잡을 수 없을 정도로 다양하지만 그 시작은 Goodfellow 의 Generative Adversarial Networks 였다.
GAN 을 처음 접할 때 가장 많이 드는 예시는 위조지폐범과 경찰의 예시다. 위조지폐범은 처음엔 지폐를 위조하는 법을 모르지만, 경찰에게 발각되는 과정을 거치며 점점 더 정교한 지폐를 위조하게 되고, 결국 경찰마저 속이는 실력을 학습한다는 간단하면서도 직관적인 모델 설명이다.
모든 강의와 모델 설명에서 똑같은 예시를 들기에 다들 약속이나 한줄 알았지만 본 논문에서 직접 든 예시였다.
GAN 은 \(G\) (Generator, 생성자), \(D\) (Discriminator, 판별자) 두개의 모델을 동시에 학습하며 \(G\) 는 \(D\)를 속이기 위해, 그리고 \(D\)는 \(G\)를 잡기 위해 학습이 된다. 이때 GAN 은 다른 생성모델에서 사용하는 마르코브 체인과 같은 stochastic 과정이 필요 없고, 딥러닝에서 익숙한 역전파를 통해 학습된다. 새로운 샘플을 생성할 때 순전파만 사용하기에 굉장히 빠르다는 장점 또한 있다.
Generative Models
우리가 익숙한 지도학습 모델들은 정답 라벨을 통해 샘플스페이스 속 데이터를 구분짓는 분류기를 학습하지만, 생성모델은 데이터의 실제 분포를 학습한다. 만약 생성모델이 데이터의 분포를 학습한다면, 해당 분포에서 확률이 제일 높은 지점에서 샘플을 추출하면 실제 데이터와 유사할 것이다. 이때 GAN 의 \(G\) 는 데이터의 실제 분포를 학습하고, \(D\) 는 \(G\) 가 생성한 샘플을 진짜인지 가짜인지 판별한다.
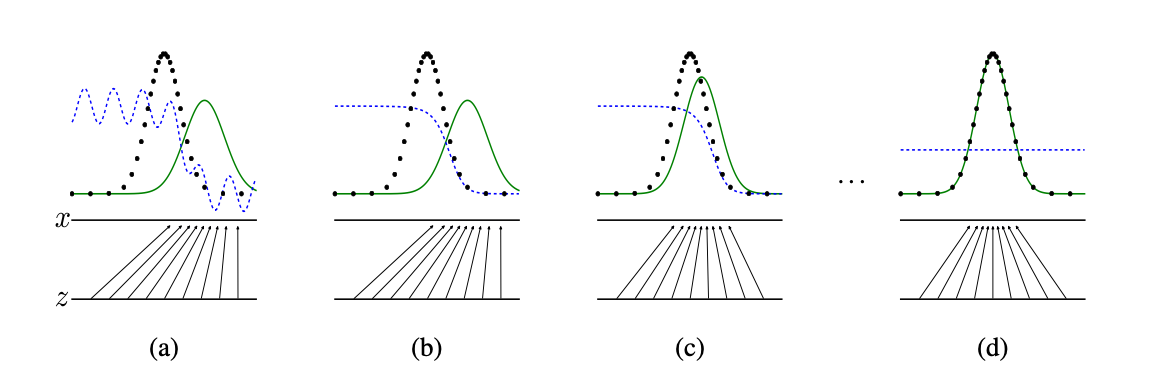
위 이미지에서 초록 분포는 생성모델 \(G\)의 분포이며, 실제 분포는 검정 점선이다. \(G\)는 latent domain 에서 sample \(z\) 를 추출하여 실제 데이터의 분포인 \(x\) 로 매핑하며, \(D\) 는 해당 샘플이 진짜면 1, 가짜면 0을 리턴하도록 학습한다.
a. 처음엔 \(G\) 는 학습이 되어있지 않아 실제 데이터 분포와 많이 다르고, \(D\) 도 학습이 잘 되어있지 않아 전반적으로 fluctuate 한다. 그럼에도 실제 데이터 분포가 내려가고 \(G(z)\) 가 올라가는 시점엔 \(D\) 는 비교적 낮게 Probability 를 측정한다.
b. 논문에선 GAN 을 학습시킬 때 \(D\) 를 먼저 학습한다. 그렇기에 전반적으로 실제 데이터 분포에 대한 P 를 균등하게 측정하고, \(G(z)\) 에 대해 거의 0에 가깝게 P 를 측정한다.
c. \(D\) 를 학습 후 \(G\) 를 학습하면, \(G(z)\) 의 분포가 실제 데이터 분포와 유사해진다.
d. 최종적으로 \(G\) 가 완벽히 실제 데이터 분포를 학습한다면, \(D\) 는 샘플이 실제 데이터인지 \(G(z)\) 인지 판별하지 못하기에 P 를 uniform 하게 0.5 로 측정한다.
최종적으로 \(G\)가 잘 학습이 된다면, \(G\) 의 분포에서 데이터 점이 아닌 부분을 추출하면 이전에 없었던 새로운 데이터가 생성되는 것이다. 즉, 우리가 알고 있는 인퍼런스 과정은 \(G\) 만 사용하는 것이다.
Objective function of GAN
\[\min _{G} \max _{D} V(D, G)=E_{x \sim p_{\text {data }}(x)}[\log D(x)]+E_{z \sim p_{z}(z)}[\log (1-D(G(z)))]\]GAN 의 목적함수 \(V\) 는 굉장히 단순하면서도 명쾌하다.
- \(D\) : Discriminator
- \(G\) : Generator
- \(x \sim p_{\text {data }}(x)\) : 실제 데이터 분포에서 샘플 \(x\) 를 추출
- \(z \sim p_{z}(z)\) : 노이즈 분포에서 latent vector \(z\) 를 추출
GAN 의 목적함수는 game theory 의 two player minmax game 에 기반한다. \(G\) 에 대해 목적함수 값을 최소화 함과 동시에 \(D\) 에 대해 목적함수의 값을 최대화 하는것이다. \(G(z)\) 는 새로운 데이터 인스턴스를 생성하고 (MNIST 데이터라면 28x28 array), \(D(x)\) 는 \(x\) 가 실제 분포에서 나왔을 확률 (0~1) 을 리턴한다. 이 사실을 알고 \(D\) 의 관점에서 목적함수를 해체해보자.
Discriminator’s Perspective: Maximize
\(D\) 는 자신이 받는 인풋이 실제 데이터 \(x\) 이면 1을 리턴해야 하고, \(G(z)\) (가짜 데이터) 면 0을 리턴해야 한다.
\[E_{x \sim p_{\text {data }}(x)}[\log D(x)]\]그렇기에 \(x\) 가 실제 데이터에서 왔다면, 목적함수의 앞부분은 이를 maximize 하는 역할을 한다.
\[E_{z \sim p_{z}(z)}[\log (1-D(G(z)))]\]반대로 \(D(G(z))\) 에 대해 0에 가까운 확률을 리턴해야 한다. \(D(G(z))\) 가 작을수록 \(log(1-D(G(z)))\) 는 커지기 때문에 목적함수의 뒷부분은 이를 maximize 하는 역할을 한다.
\[+\nabla_{\theta_{d}} \frac{1}{m} \sum_{i=1}^{m}\left[\log D\left(\boldsymbol{x}^{(i)}\right)+\log \left(1-D\left(G\left(\boldsymbol{z}^{(i)}\right)\right)\right)\right]\]그렇기에 학습을 진행 할 때 1차 도함수의 양의 방향으로 학습을 진행한다.
Generator’s Perspective : Minimize
반대로 \(G\) 는 목적함수에 대해서 최소화 해야 한다. 목적함수의 앞부분은 \(G\)가 없기 때문에 상수취급을 할 수 있으므로, 결국 목적함수의 뒷부분만 남는다.
\[E_{z \sim p_{z}(z)}[\log (1-D(G(z)))]\]\(G\) 는 \(D\)를 속이는것이 목표다. \(D\) 가 ‘속는다’ 라는 표현은 곧 \(D(G(z))\) 가 1에 가까워지는 것을 의미하므로, 목적함수를 minimize 하는것이 된다.
\[-\nabla_{\theta_{g}} \frac{1}{m} \sum_{i=1}^{m} \log \left(1-D\left(G\left(\boldsymbol{z}^{(i)}\right)\right)\right)\]그렇기에 학습을 진행 할 때 1차 도함수의 음의 방향으로 학습을 진행한다.
Global Optimality
결국 GAN 은 위와 같은 간단한 목적식을 통해 생성자를 학습시킨다. 생성자를 학습시킨다는 것은 결국 생성자의 분포와 실제 분포가 같아진다는 것을 의미하는데, 논문은 이에 대해 증명을 한다.
명제: \(G\) 가 고정된 상황에서 \(D\) 의 optima 는 \({p_{data}(x)\over p_{data}(x)+ p_g(x)}\) 이다.
증명: 목적식에서 Expectation 을 공식으로 바꿔보면 다음과 같다: (\(E = \int xf(x)dx\))
\[\begin{aligned} V(G, D) &=\int_{\boldsymbol{x}} p_{\mathrm{data}}(\boldsymbol{x}) \log (D(\boldsymbol{x})) d x+\int_{\boldsymbol{z}} p_{\boldsymbol{z}}(\boldsymbol{z}) \log (1-D(g(\boldsymbol{z}))) d z \end{aligned}\]이때 \(D\) 의 입장에서 \(G(z)\) 나 \(x\) 는 그저 판별해야하는 인풋일 뿐이기에, \(g(z)=x\) 다. 그렇다면 위의 식을 하나의 적분식으로 표현 할 수 있다.
\[\begin{aligned} V(G, D) &=\int_{\boldsymbol{x}} p_{\mathrm{data}}(\boldsymbol{x}) \log (D(\boldsymbol{x}))+p_{g}(\boldsymbol{x}) \log (1-D(\boldsymbol{x})) d x \end{aligned}\]이때 위 식은 \(y = alog(y)+blog(1-y)\) 의 꼴을 띄고 있다. 이 식의 maximum 은 \([0,1]\) 사이에서 \(a\over a+b\) 이기 때문에, \(D\) 의 optima 또한 \({p_{data}(x)\over p_{data}(x)+ p_g(x)}\) 이다.
위의 증명을 통해 최종적으로 \(p_g=p_{data}\) 인 것을 증명할 수 있다.
명제: Global optimum 은 \(p_g=p_{data}\) 이다.
증명: \(G\) 가 고정된 상황에서 \(G\) 에 대한 새로운 학습 criterion 함수 \(C\) 를 정의한다.
\[\begin{aligned} C(G) &=\max _{D} V(G, D) \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}}\left[\log \left(1-D_{G}^{*}(G(\boldsymbol{z}))\right)\right] \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }} a}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \left(1-D_{G}^{*}(\boldsymbol{x})\right)\right] \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log \frac{p_{\text {data }}(\boldsymbol{x})}{P_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \frac{p_{g}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right] \end{aligned}\]첫번째 명제에서 얻은 \({p_{data}(x)\over p_{data}(x)+ p_g(x)}\) 를 대입한 형태로 \(C(G)\) 를 표현한다.
\[\begin{aligned} C(G)= \mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log \frac{2*p_{\text {data }}(\boldsymbol{x})}{P_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \frac{2* p_{g}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right] - log(4) \end{aligned}\]이때 약간의 수학적인 trick 을 이용해 앞단과 뒷단에 2를 곱한 뒤, \(log(4)\) 를 빼줌으로써 이를 상쇄시킨다.
\[C(G)= K L\left(p_{\text {data }} \| p_{g}\right)=\int_{-\infty}^{\infty} p_{\text {data }}(x) \log \left(\frac{p_{\text {data }}(x)}{p_{g}(x)}\right) d x\]이때 식의 앞단과 뒷단은 KL Divergence 의 공식과 형태가 같아지기 때문에, 이를 KL Divergence 형태로 표현한다.
\[C(G)= \left.K L\left(p_{\text {data }} \| \frac{\mathrm{p}_{\text {data }}(\mathrm{x})+\mathrm{p}_{\mathrm{g}}(\mathrm{x})}{2}\right)\right)+K L\left(p_{g} \| \frac{\mathrm{p}_{\mathrm{data}}(\mathrm{x})+\mathrm{p}_{\mathrm{g}}(\mathrm{x})}{2}\right)-\log (4)\]KL Divergence 는 두 분포의 유사도를 측정하는데 사용하지만 distance metric 으로 사용하긴 어렵기에 Jensen-Shannon Divergence 로 치환한다.
\[C(G)= 2*JSD(p_{data}||p_g) - log(4)\]JSD 는 distance metric 이므로 \(p_g=p_{data}\) 일때 JSD=0 이다. 그렇기에 \(C(G)\) 의 global optimum 은 \(-log(4)\) 이며, 유일한 해답은 \(p_g=p_{data}\) 이다.