Dimensionality Reduction and the Genetic Algorithm
Contents
-
Introduction
-
The Curse of Dimensionality
-
Dimensionality Reduction
-
Supervised Feature Selection Algorithms
- Exhaustive Search
- Forward Selection
- Backward Elimination
- Stepwise Selection
-
Performance Metrics
- Akaike Information Criterion
- Bayesian Information Criterion
-
Genetic Algorithm
- Metaheuristics from Biomimicry
- Step 1: Initialization
- Step 2: Training and Fitness Evaluation
- Step 3: Selection
- Step 4: Crossover and Mutation
- Step 5: Iteration and Final Solution
해당 포스트는 2021년 1학기 고려대학교 강필성 교수님의 ‘다변량분석’ 강의를 참고하여 작성되었습니다.
이미지는 강필성 교수님의 강의 슬라이드에서 발췌하였습니다.
A+ 감사했습니다 교수님
Introduction
머신러닝 모델을 구축할 때 raw data 를 바로 학습시키는 경우는 드물다. 학습을 진행하기 전 주어진 데이터에 대한 전처리를 진행하는데, 이는 보통 outlier 제거, 정규화, 그리고 차원축소로 이루어진다. 차원축소란 기존 데이터셋에 존재하는 설명변수들의 개수를 줄이는 것인데, 이때 생성될 모델에 대해 성능 저하없이 차원을 축소하는것이 핵심이다.
앞서 예시로 들었던 tabular data 는 설명변수가 많아봤자 20개였지만, 실생활에서 접하는 데이터셋의 설명변수의 수는 상상을 초월한다. 예시로 NLP 의 가장 고전적인 방법론 중 하나인 BoW (Bag of Words) 를 들어보자. BoW 방법론으로 문서를 데이터화한다면, 변수의 개수는 해당 문서가 작성된 언어에 존재하는 단어의 개수이다. 즉, 한국어로 작성된 문서를 BoW 방법론으로 tabular data 로 바꾼다면, column 의 수는 약 100만개가 될 것이다. Sparsity 는 둘째치고, computational complexity 는 상상을 초월할 것이다.
The Curse of Dimensionality
데이터마이닝에서 Curse of Dimensionality (차원의 저주) 라는 표현은 자주 등장한다. 이는 한 데이터셋/모델의 변수의 수가 선형적으로 증가한다면, 동일한 설명력을 유지하기 위해서 객체 (sample) 의 수는 기하급수적으로 증가한다는 논리다.
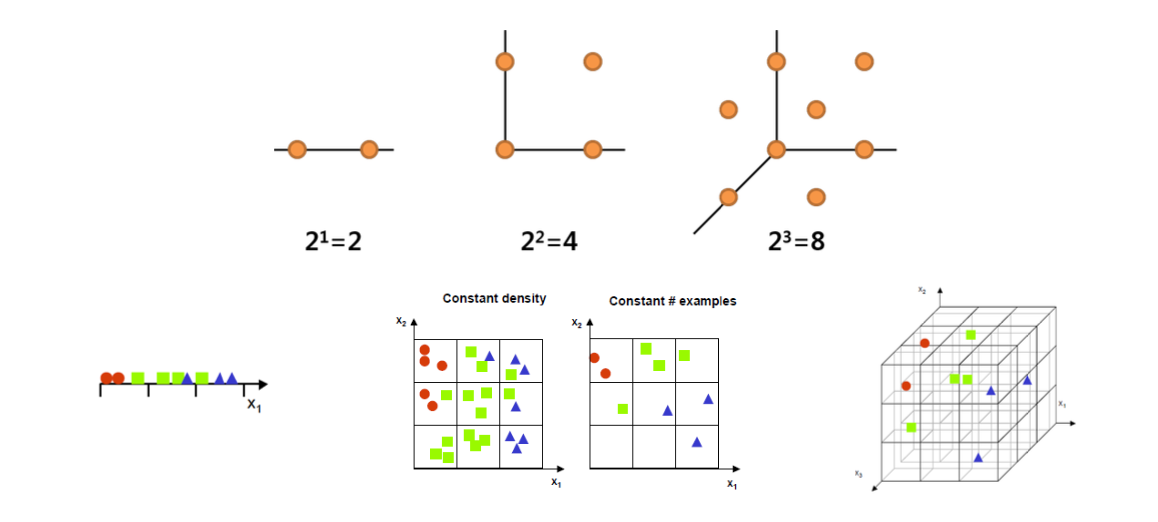
예시를 들어보자. 첫번째 그림에서 ‘점 사이의 거리는 1이다’ 라는 정보를 담은 모델이다. 만약 이 모델에서 변수의 수가 1개에서 2개로 늘어난다면, ‘점 사이의 거리는 1이다’ 라는 정보를 보존하기 위해 점의 개수는 4개로 늘어나야하고, 변수가 3개라면 점은 8개로 늘어나야 한다. 일반화를 하면 \(n\) 차원의 모델이 정보를 보존하기 위해선 \(2^n\) 개의 sample 이 필요할 것이다. 모델을 학습시킬 때 고차원의 데이터를 사용한다면 생기는 문제는 다음과 같다.
- 데이터 속 noise 가 들어있을 확률이 높아진다. 이는 예측력을 저하시키는 주된 원인이다.
- Computational Complexity 가 늘어난다.
- 일반화된 예측력을 가진 모델을 학습시키기 위해 기하급수적으로 많은 sample 수가 필요하다.
- 변수간 독립성을 보장하지 못한다.
이론적으론, 변수의 수가 많을수록 모델의 성능은 향상된다. 하지만 이는 iid 의 조건 하에 라는 거의 만족 불가능한 조건을 전제로 두고 있기 때문에, 변수간의 상관성과 noise 에 의해 모델의 예측력이 저하되는게 현실이다.
Intrinsic Dimension
사용되는 데이터셋의 실제 차원의 수보다 낮은 저차원으로도 데이터셋의 본질적인 개념을 표현할 수 있는 차원을 Intrinsic Dimension 이라고 한다. 예시로 MNIST 데이터셋은 16 by 16 pixel, 즉 256차원의 데이터이지만 ISOMAP 으로 2차원으로 차원축소를 한 뒤 시각화를 진행해도 문제없이 분류선을 그을 수 있다. 즉, 이미지 데이터가 픽셀 수에 따라 차원이 결정되지만 이는 딥러닝에서 사용되는 행렬연산 때문에 우리가 직접 256차원으로 변환해서 계산하는 것 뿐이다. 본질적으로 2차원으로 이미지를 표현 할 수 있기 때문에 이미지의 Intrinsic Dimension 은 2차원이다.
Dimensionality Reduction
앞서 설명한 것 처럼 전처리 과정에서 차원축소를 거의 필수적으로 해야 하는데, 차원축소는 크게 3가지 방법으로 나눌 수 있다.
- Utilize domain knowledge. 해당 분야의 전문가들이 중요도가 낮은 변수를 수작업으로 제거한다.
- Employ a quantitative reduction technique. 변수의 중요도에 따라 변수를 선택한다.
- Use a regularization term in the objective function. Shrinkage methods 라고도 불리며, 목적함수 (cost function) 가 적은 수의 변수를 선호하도록 일종의 장치를 걸어둔다.
또한 차원축소 방법론은 크게 2가지로 나눌 수 있다.
-
Supervised Dimensionality Reduction
지도학습 차원축소법이라고도 하며, 학습 알고리즘의 결과에 따른 변수선택에 feedback loop 을 사용하는 방법론이다. 학습시키고자 하는 모델의 cost function 을 그대로 차용하기도 한다. 이때 feedback loop 에 사용된 학습 알고리즘에 따라 선택된 (혹은 제거된) 변수들이 달라진다. 이번 장에서 다루는 알고리즘들이 지도학습 차원축소법에 해당된다.
-
Unsupervised Dimensionality Reduction
비지도학습 차원축소법은 지도학습 차원축소법과는 다르게 학습 알고리즘의 결과에 의존하지 않고 feedback loop 또한 없다. 고차원의 데이터의 정보량을 유지한 채 저차원의 좌표계에 투영하는 방법론이다. 만약 사용된 모델과 방법론이 동일하다면 항상 같은 결과가 나온다는 특징 (closed form solution) 이 있고, 대표적으로 PCA Analysis, ISOMAP, Manifold based 알고리즘들이 있다.
차원축소를 진행 할 시, 크게 두가지 형태로 기존 변수의 set 에서 새로운 subset 을 만든다.
-
Feature Selection
변수선택법은 기존 변수들의 집합에서 설명력이 높은 변수들만 골라 새로운 집합을 사용하는 방법이다. 이때 변수들은 그대로 유지된다. 이번 장에서 다루는 알고리즘들은 변수선택법에 해당된다.
-
Feature Extraction
변수추출법은 기존 변수들의 조합으로 기존 집합에 존재하지 않는 새로운 변수들을 생성해내는 방법이다.
Supervised Feature Selection Algorithms
- Exhaustive Search
- Forward Selection
- Backward Elimination
- Stepwise Selection
Exhaustive Search
가장 원초적인 변수선택으로 인한 차원축소법이며, brute force algorithm 에 해당된다. 다중선형회귀분석 모델에 사용된 데이터셋을 차원축소하는 예시를 들어보자. 만약 3개의 변수 중 가장 좋은 조합의 변수들을 사용한다면, 총 7개의 조합으로 회귀계수를 구한 뒤 평가지표를 비교해야 한다. 만약 \(n\) 개의 변수간 조합을 비교한다면, 총 \(2^n - 1\) 개의 회귀모델을 비교해야 할 것이다 (모든 변수를 사용 안하는 경우를 제외하여 \(-1\)).
Exhaustive Search 는 전역탐색기법이기 때문에 항상 최적해를 보장하지만, \(O(2^n)\) 의 time complexity 라는 치명적인 단점이 존재한다.
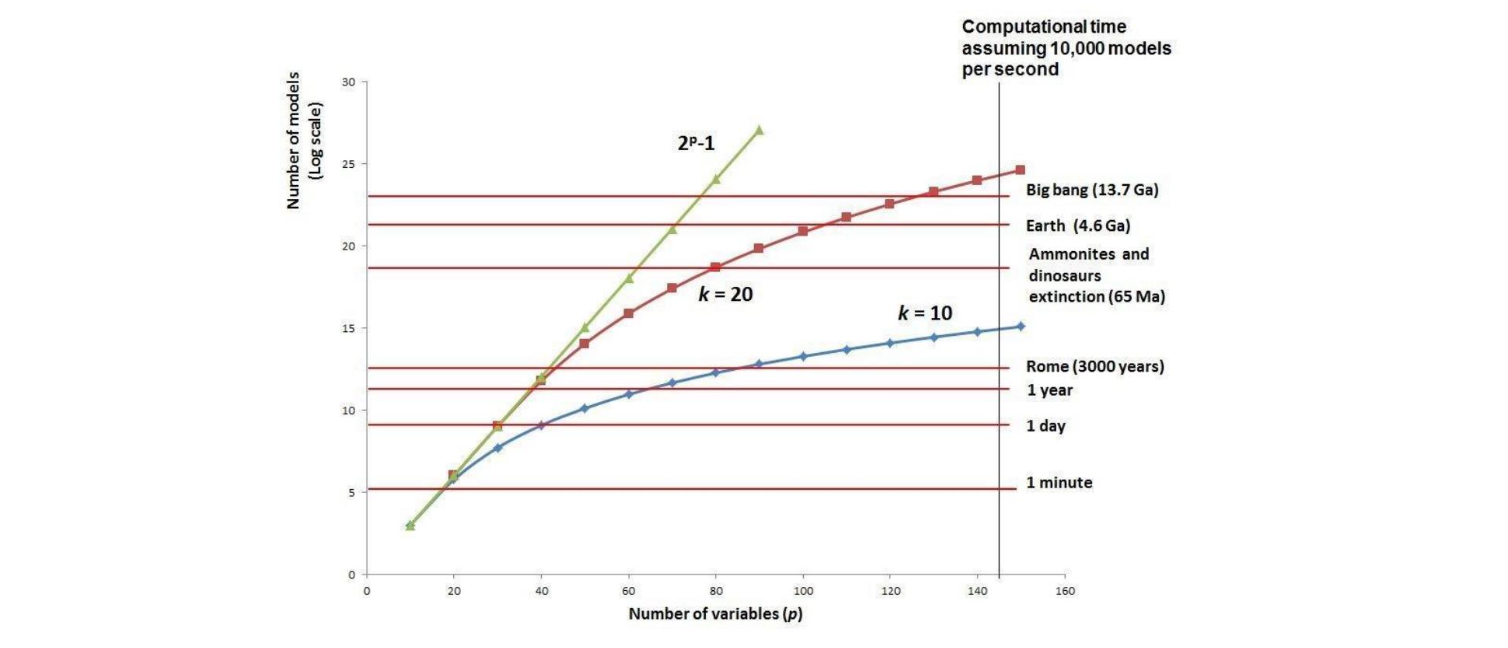
초당 1만개의 모델을 검증할 수 있는 컴퓨터로 Exhaustive Search 를 진행해본다고 하자. 탐색해야 하는 변수의 수가 20개라면 걸리는 시간은 약 1분 남짓이다. 하지만 변수의 수가 40개로 늘어나면 1년이 걸리고, 80개로 늘어난다면 우주의 근원부터 현재까지의 시간이 지나도 알고리즘은 완료되지 않는다. 즉 Exhaustive Search 는 변수가 20개 이상 넘어간다면 쓰지 않는게 좋다.
Forward Selection
Exhaustive Search 는 전역최적해를 보장하지만 time complexity 때문에 실 사용이 어렵다. 그렇기에 성능을 조금 희생하는 대신 time complexity 를 확연히 줄여주는 알고리즘인 전진선택법을 알아보자. 전진선택법은 먼저 변수가 없는 모델에서 시작을 한다. 이때 한 iteration 마다 기존 변수의 집합 중 한개씩 사용하여 모델을 만든 뒤, 성능이 제일 좋은 변수를 선택한다. 새로 변수를 선택해도 성능이 증가하지 않을 시 종료조건을 달성하고, 알고리즘은 종료된다. 이때 선택된 변수는 제거되지 않는다는 특징 (비복원추출) 을 가지고 있고, 점진적으로 모델에 사용되는 변수의 수는 증가한다.
\[y=f(x_1) \rightarrow y=f(x_1,x_5) \rightarrow y=f(x_1,x_5,x_3)\rightarrow \ ...\]Backward Elimination
후방소거법은 전진선택법의 정 반대로 알고리즘이 수행된다. 모든 변수를 사용한 모델에서 시작되며, 변수를 한개씩 소거해 가며 모델의 성능을 비교한다. 변수 소거시 성능이 오히려 오르거나 변화가 크게 없을 시 해당 변수를 완전히 소거하고 다음 iteration 으로 나아간다는 특징이 있다. 전진선택법과 동일하게 비복원추출로 진행되며, 변수 소거 시 성능이 급격히 떨어지면 종료조건을 만족한다.
\[y=f(x_1,x_2,...,x_d) \rightarrow y=f(x_1,x_2,x_3)\]Stepwise Selection
단계적 선택법은 전진선택법과 후방소거법을 합친 알고리즘이다. 앞선 두 알고리즘과 다르게 한번 제거된 변수는 다시 선택될 수 있으며, 한번 선택된 변수는 다시 제거가 될 수 있다는 특징을 가지고 있다. 그렇기에 FS/BE 보단 더 높은 time complexity 를 요구하지만 더 나은 성능을 보인다는 장점을 가지고 있다.
Performance Metrics
위에 소개한 4개의 차원축소 알고리즘은 지도학습 차원축소방법론이고, 선택된 변수들의 performance metric 에 따라 feedback loop 을 제공함으로써 최적의 변수들을 도출해낸다. 사용된 모델에 따라 performance metric 은 상이할 수 있지만, 회귀모델에서 사용되는 성능평가지표를 그대로 사용 할 수 있다.
Akaike Information Criterion
\[AIC = n \cdot ln({SSE \over n}) + 2k\]AIC 는 기본적인 SSE 에 변수에 수에 따른 penalty 를 부여하는 성능평가지표다. \(n\) 은 sample size, \(k\) 는 변수의 수다. 본질적으로 cost function 처럼 작동하기 때문에 AIC 는 낮을수록 좋다. 그렇기에 AIC 식의 앞부분이 의미하는 것은 ‘두 모델간 변수의 수가 같다면 성능이 높은 모델 선택’ 이고, 뒷부분이 의미하는 것은 ‘두 모델간 성능이 동일하다면 변수의 수가 적은 모델 선택’ 이다.
Bayesian Information Criterion
\[BIC = n \cdot ln({SSE \over n}) + {2(k+2)n\sigma^2 \over SSE} - {2n^2\sigma^4\over SSE^2}\]BIC 는 AIC에 추가 항이 붙은 성능평가지표로, 모든 변수를 포함한 모델의 샘플들의 표준편차를 사용한다는 특징이 있다.
이외에도 다중선형회귀분석에서 살펴본 Adjusted \(R^2\) 도 성능평가지표로 사용할 수 있다.
Genetic Algorithm
Exhaustive Search 는 전역최적해를 보장하지만 time complexity 때문에 사용하기가 어렵다. 그에 반해 FS, BE, SS 는 성능을 약간 포기하는 대신 time complexity 를 대폭 줄인다. 하지만 FS, BE, SS 의 search space 는 local 에서 머물기 때문에, global optima 를 절대 찾을 수 없을 가능성이 존재한다. 반면 Time complexity 는 더 높지만 mutation 을 통해 local optima 를 벗어나 global optima 를 찾을 수 있는 알고리즘이 그 유명한 Genetic Algorithm 이다.
Metaheuristics from Biomimicry
유전 알고리즘은 효율적인 trial and error 을 통한 메타휴리스틱 방법론 중 하나다. 유전 알고리즘은 이름에서도 알 수 있듯이 Biomimicry 를 통해 고안된 알고리즘이다.
Biomimicry
Biomimicry 란 자연에서 볼 수 있는 디자인적 요소들이나 생물체의 특성들을 연구 및 모방하는 분야다. 딥러닝의 초기 모델인 인공신경망은 사람의 뇌의 Biomimicry 모델이며, 최적화 이론에선 유전 알고리즘, Ant Colony Algorithm, Particle Swarm Optimization 등이 대표적인 Biomimicry 방법론들이다.
The world is poorly designed. But copying nature helps. Vox 에서 만든 Biomimicry 에 대한 영상이다. 굉장히 흥미롭다.
유전 알고리즘은 환경에 특화되고 가장 우월한 개체만 다음 세대로 유전자를 남긴다는 다윈의 자연선택설에 기초한다. 열등한 유전자는 자연스럽게 도태되는 아이디어를 그대로 가져와 Selection, Crossover, Mutation 과정을 거쳐 가장 우월한 ‘유전자’, 즉 설명변수를 최종적으로 구하는 알고리즘이다.
Step 1: Initialization
유전 알고리즘의 첫 단계는 초기값 설정, 혹은 Encoding 이다. 유전 알고리즘은 머신러닝 이외에도 다양한 분야에서 사용되기 때문에 Encoding 방법론은 분야마다 상이하지만, 차원축소에서 사용되는 유전 알고리즘에선 Binary Encoding 이 사용된다.
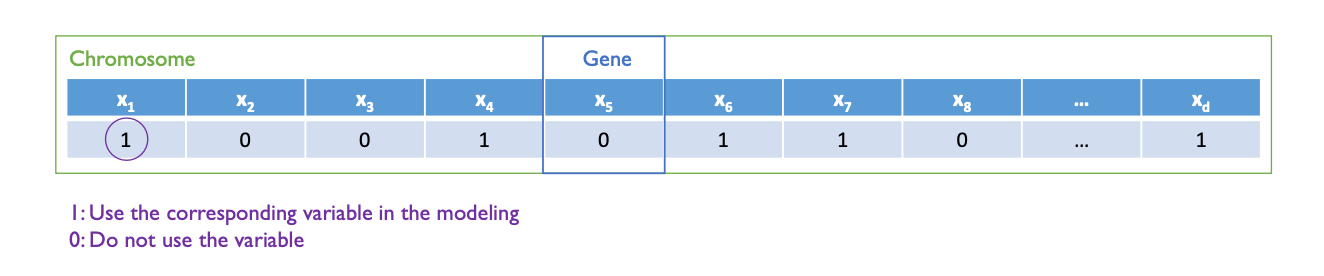
유전 알고리즘에서 사용되는 용어는 위와 같다. 하나의 chromosome 은 데이터셋이 가지고 있는 변수의 수 만큼 Gene 을 가지고 있으며, 처음 알고리즘을 시작할 때 랜덤하게 각 Gene 에 0 혹은 1 의 Binary 값이 주어진다. 알고리즘의 최종 output 은 하나의 chromosome 이며, 1로 활성화 되어있는 Gene 을 사용한다.
Parameter Initialization
- Population Initialization: Hyperparameter 로, 알고리즘에 사용할 chromosome 의 개수를 설정한다. 보통 50~100개의 chromosome 을 사용한다.
- Fitness Function: 각 chromosome 의 성능, 혹은 ‘우월성’ 을 판별하기 위한 평가지표다. 학습하고자 하는 모델의 loss function 을 사용한다 (ex. MLR = \(R^2, AIC\))
- Crossover Mechanism: Hyperparameter 로, 몇개의 crossover point 로 알고리즘을 진행할지 정한다.
- Mutation Rate: Hyperparameter 로, chromosome 의 gene 이 반대값으로 활성화/비활성화 될 확률이다. 보통 0.01 (1%) 를 사용한다.
- Stopping Criteria: 알고리즘의 종료조건이다. 한 세대에서 다음 세대로 넘어갈때 fitness function 의 증가값이 특정 범주를 넘지 못하거나, 설정한 세대까지 진화를 했다면 멈추도록 설정 할 수 있다.
Step 2: Training and Fitness Evaluation
Hyperparameter 로 설정한 population 만큼 모델을 학습시키는 과정이다. 이때 데이터셋의 모든 변수를 사용하지 않고, 한 chromosome 에 활성화 된 변수만 가지고 학습을 시킨다. 이때 지정한 fitness function 의 값은 해당 chromosome 의 ‘우월성을 나타낸다.’ 앞서 언급한 것 처럼 MLR 은 \(R^2\) 같은 fitness function 을 사용하지만, 대부분의 fitness function 은 같은 원리로 작동한다.
- 두개의 chromosome 이 같은 fitness value 를 가지고 있다면, 활성화 된 gene 이 적은 chromosome 에게 가중치 부여
- 두개의 chromosome 이 같은 활성화 된 gene 의 수를 가지고 있다면, 예측성능이 더 높은 chromosome 에게 가중치 부여
\(R^2, AIC, BIC\) 산출식에서 이 원리를 확인 할 수 있다.
Step 3: Selection
Population 만큼 모델이 학습된 후 각 모델의 fitness function 까지 산출 되었다면, 다음 세대로 gene 을 넘길 chromosome 을 선택하는 단계다. 이때 선택 방법은 두가지가 있다.
-
Deterministic selection
Fitness function 상 상위 N% 의 chromosome 만 선택한다. 이때 하등한 chromosome (100-N)% 는 절대 선택이 되지 않는다.
-
Probabilistic selection
각 chromosome 의 fitness function 을 가중치로 부여하고 선택하는 방법이다. 이로써 모든 chromosome 은 아무리 열등하더라도 다음 세대로 gene 을 넘길 가능성이 생긴다. 예로, 3개의 chromosome A,B,C 가 있고 각각의 fitness function 은 3, 1, 2 다. 그렇다면 A 가 선택될 확률은 3/6, B 가 선택될 확률은 1/6, C 가 선택될 확률은 2/6이 된다. Probabilistic selection 을 사용한다면 Deterministic Selection 에서 정한 것 처럼 총 population 의 몇% 를 선택할지 또한 정해야 한다.
Step 4: Crossover & Mutation
Crossover 가 다음 세대로 gene 을 넘기는 부분이다. 두개의 parent chromosome 은 두개의 child chromosome 을 생성한다.
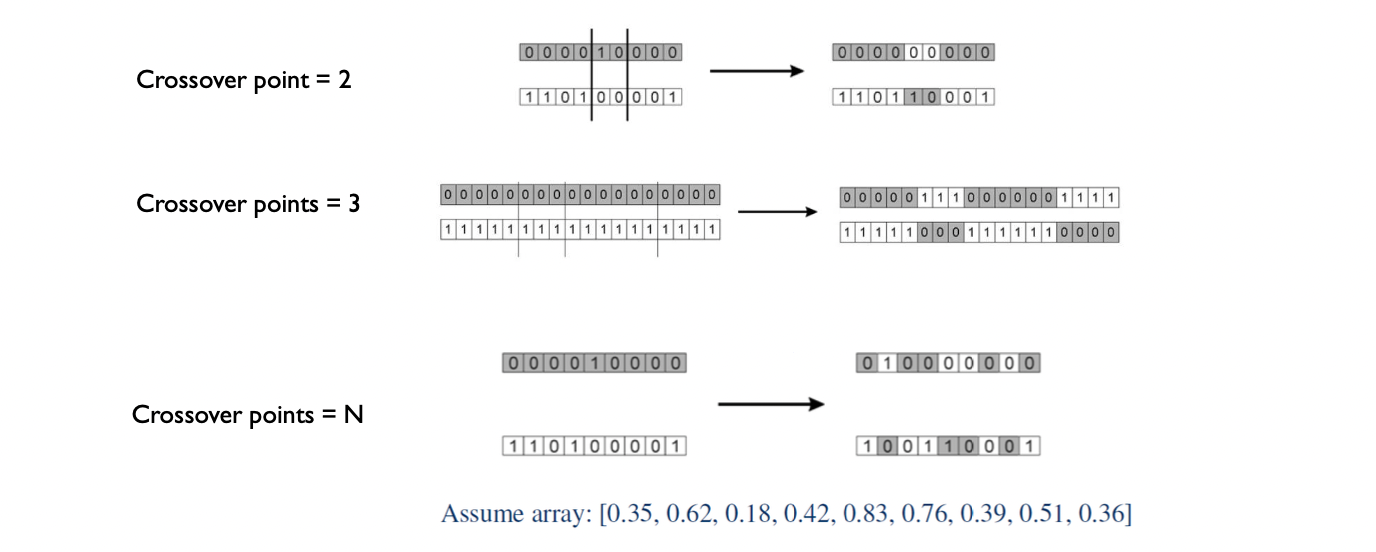
Child chromosome 이 생성되는 과정은 위와 같다. Initialization 단계에서 지정한 hyperparameter 인 crossover point 에 따라 각 부모 chromosome 에 분기가 생기며, 해당 분기 속 gene 들이 서로 바꿔치기 되며 child chromosome 이 생성된다. Crossover point 는 1개부터 \(n\) 개로 설정 할 수 있으며, 만약 \(n\) 개로 설정했다면 gene 의 개수만큼 난수를 담은 array 를 생성한다. Array 의 index 값이 0.5가 넘는다면 chromosome 의 해당 index 의 gene 을 부모끼리 교환한다. 실제로 Crossover point 는 \(n\) 개로 설정하는 경우가 많다.
Crossover 를 통해 child chromosome 이 생성되었다면, 아주 낮은 확률로 mutation 이 일어난다. 앞서 설정한 hyperparameter 에 따라 각 Gene 의 값이 반대값으로 바뀌도록 장치를 설정한 것인데, 이는 각 chromosome 이 local optima 에서 벗어날 기회를 제공한다. 이때 mutation rate 을 너무 크게 설정한다면 convergence time 이 늘어날 수도 있다. 보통 mutation rate 은 0.01 로 설정한다.
Step 5: Iteration and Final Solution
Initialization 후 학습이 진행되며 fitness value 에 따라 selection 을 진행 한 뒤, crossover 와 mutation 까지의 과정을 one iteration 으로 계산한다. 유전 알고리즘의 종료 조건은 몇번의 iteration 이거나 fitness value 의 증가분이기 때문에, 언젠간 알고리즘은 종료된다. 이후 최종적으로 남은 chromosome 들 중 가장 높은 fitness value 를 가진 chromosome 을 선택해 활성화된 gene 을 설명변수로 사용함으로써 차원축소가 완료된다.
일반적으로 fitness value 의 급격한 improvement 는 초기 iteration 에 일어나고, 몇 세대가 지난 후 plateau 한다.