Bias-Variance Decomposition

Contents

• Introduction
• Mathematical Definition
• Decomposition of Expected Test Error

해당 포스트는 Cornell CS4780 SP17 Killian Weinberger 교수님의 강의를 참고하였습니다.

Introduction

Bias-Variance Decomposition 은 모델의 일반화 성능을 높히기 위한 정규화 방법론들과 앙상블 방법론들의 이론적 배경이다. 실제 데이터로 학습되는 모든 모델은 어느정도의 Bias-Variance tradeoff 가 존재하기 때문에, 머신러닝을 공부 할 때 확실히 이해하고 넘어가야 하는 부분이다.

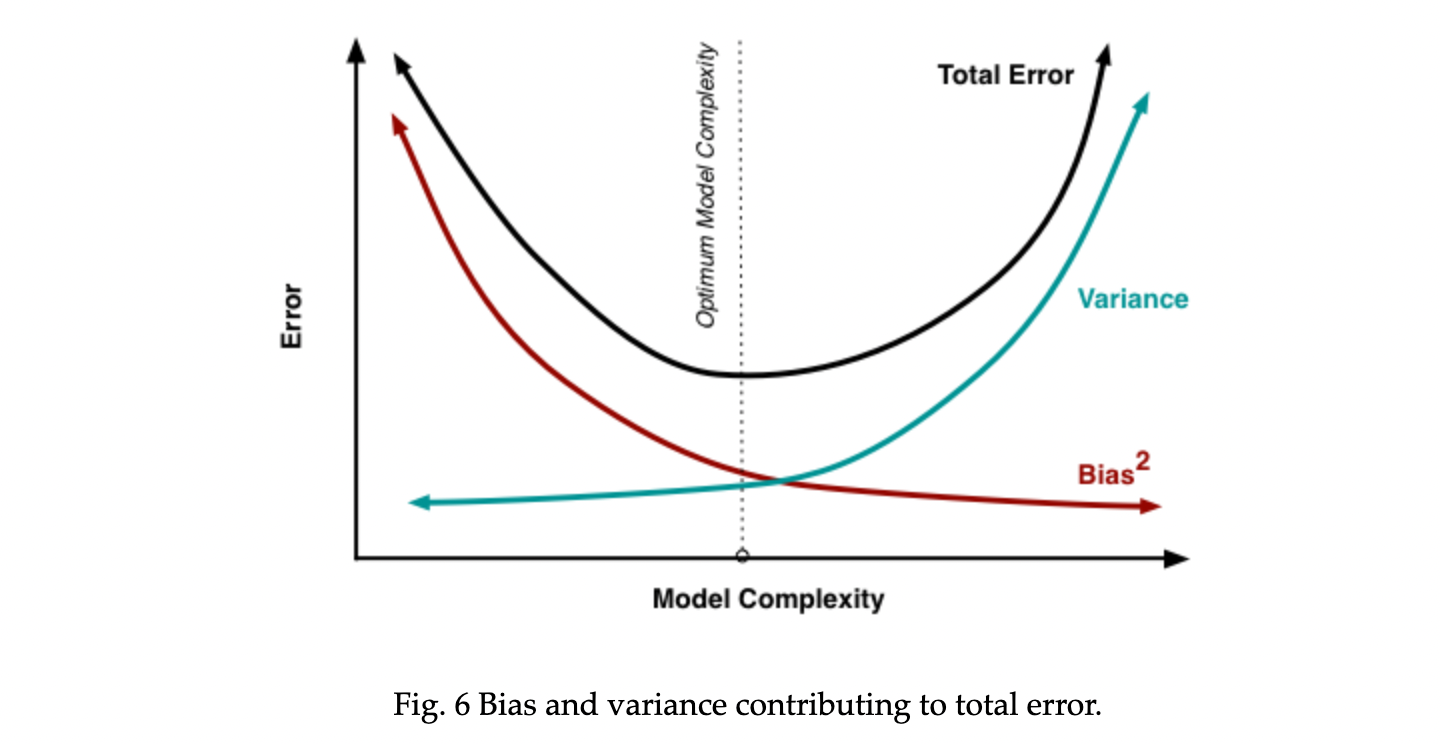
Error Due to Bias: 모델의 Expected prediction 과 실제 값의 차이다. 모델의 Expected prediction 이란 말이 생소하지만, 같은 분포에서 나온 많은 데이터셋을 통해 많은 모델을 학습시켰을 때 해당 모델들의 평균 예측치다.

Error Due to Variance: 같은 분포에서 나온 많은 데이터셋을 통해 모델을 학습시켰을 때, 한 데이터포인트에 대한 전체 평균 예측치와 개별 모델의 예측치의 차이를 의미한다. 즉, 전체 모델들간의 예측치의 차이로 해석할 수 있다.

조금 더 쉽게 풀자면, Bias 는 모델들의 전반적인 성능이 좋은지 나쁜지를 의미하고, Variance 는 각 모델들이 서로와 얼마나 다른지를 의미한다. 머신러닝의 대부분의 모델은 둘중 하나가 높다는 특징을 가지고 있기 때문에 Bias-Variance Tradeoff 라고 불린다.

특정 모델을 학습시켰을 때 test error 는 필연적으로 등장한다. Bias-Variance Decomposition 은 해당 error 가 Bias 에서 온 error 인지, variance 에서 온 error 인지, noise 에서 온 error 인지 평가해 줄 수 있다.

Mathematical Definition

\(P(X,Y)\) 라는 분포에서 i.i.d 로 데이터셋 \(D = \{(\mathbf{x}_1, y_1), \dots, (\mathbf{x}_n,y_n)\}\) 를 추출했다고 가정하자. Regression 모델을 가정했을 때, 모든 벡터 \(\mathbf{x_n}\) 에 대한 정답 라벨 \(y_n\) 은 unique 하지 않고, 분포에 따라 주어진다.

영상에서 이 부분에 대해 갸우뚱하는 학생들을 위해 교수님이 직접 예시를 들어준다. 집에 대한 가격을 나타내는 데이터셋에 대해, 설명변수의 값이 모두 동일한 두개의 집은 무조건적으로 가격이 같지 않다.

Expected Label:

\[\bar{y}(\mathbf{x}) = E_{y \vert \mathbf{x}} \left[Y\right] = \int\limits_y y \, \Pr(y \vert \mathbf{x}) \partial y\]

i.i.d 로 추출한 수많은 데이터셋들에 대해 모델을 학습시킨 뒤, 새로운 샘플 \(\mathbf{x}\) 에 대한 expected label 은 위와 같이 계산할 수 있다. 데이터셋 자체를 \(P(X,Y)\) 라는 분포에서 i.i.d 추출했기 때문에 random variable 로 취급할 수 있으므로, continuous r.v. 의 Expectation 을 구하는 것과 동일하게 \(y\) 값과 모델의 예측치들에 대해 \(y\) 로 미분해주면 된다.

Expected Test Error (given \(h_D\)):

\[E_{(\mathbf{x},y) \sim P} \left[ \left(h_D (\mathbf{x}) - y \right)^2 \right] = \int\limits_x \! \! \int\limits_y \left( h_D(\mathbf{x}) - y\right)^2 \Pr(\mathbf{x},y) \partial y \partial \mathbf{x}.\]

\(D\) 라는 학습 데이터를 통해 알고리즘 \(\mathcal{A}\) 를 학습시켰다고 가정하자 (\(h_D = \mathcal{A}(D)\)). 그렇다면 해당 모델 \(h_D\) 의 Expected Test Error 은 (예시가 regression 이기 때문에 squared loss 사용) 위와 같이 구할 수 있다. \(D\) 는 앞서 설명했듯이 random variable 로 취급할 수 있고, \(h_D\) 는 \(D\) 에 대한 function 이기 때문에 마찬가지로 random variable 이다.

Expected Classifier (given \(\mathcal{A}\)):

\[\bar{h} = E_{D \sim P^n} \left[ h_D \right] = \int\limits_D h_D \Pr(D) \partial D\]

\(h_D\) 와 \(\mathcal{A}\) 를 구분짓는게 핵심이다. \(h_D\) 는 하나의 모델이고 \(\mathcal{A}\) 는 학습될 수 있는 모든 모델이다. 그렇기 때문에 위와 같이 expected classifer 은 분포 \(P\) 에서 추출된 \(D\) 로 학습된 모든 모델의 expectation 이라고 할 수 있다.

Expected Test Error (given \(\mathcal{A}\)):

\[\begin{equation*} E_{\substack{(\mathbf{x},y) \sim P\\ D \sim P^n}} \left[\left(h_{D}(\mathbf{x}) - y\right)^{2}\right] = \int_{D} \int_{\mathbf{x}} \int_{y} \left( h_{D}(\mathbf{x}) - y\right)^{2} \mathrm{P}(\mathbf{x},y) \mathrm{P}(D) \partial \mathbf{x} \partial y \partial D \end{equation*}\]

모든 모델에 대한 expectation 을 구했기 때문에 이제 가능한 모든 모델에 대한 expected error 을 표현 할 수 있다. 우리의 목적은 \(P(X,Y)\) 에서 추출된 \(D\) 로 학습된 모델 \(\mathcal{A}\) 의 expected 성능을 구하는 것이기 때문에, 위 식이 이를 나타낸다. 이때 해당 식을 decompose 하면 정확히 어떻게 모델의 에러가 구성되어있는지 볼 수 있다.

Decomposition of Expected Test Error (given \(\mathcal{A}\))

\[E_{\mathbf{x},y,D}\left[\left[h_{D}(\mathbf{x}) - y\right]^{2}\right] \\ \\ = E_{\mathbf{x},y,D}\left[\left[\left(h_{D}(\mathbf{x}) - \bar{h}(\mathbf{x})\right) + \left(\bar{h}(\mathbf{x}) - y\right)\right]^{2}\right] \\\\ = E_{\mathbf{x}, D}\left[(\bar{h}_{D}(\mathbf{x}) - \bar{h}(\mathbf{x}))^{2}\right] \\ +2 \mathrm{\;} E_{\mathbf{x}, y, D} \left[\left(h_{D}(\mathbf{x}) - \bar{h}(\mathbf{x})\right)\left(\bar{h}(\mathbf{x}) - y\right)\right] \\ +E_{\mathbf{x}, y} \left[\left(\bar{h}(\mathbf{x}) - y\right)^{2}\right]\]

첫 식은 위에서 구한 Expected Test Error 이다. 이때 expectation 안에 모델의 label 의 expectation \(\bar{h}(\mathbf{x})\) 를 한번씩 빼주고 더해준다. 이를 binomial expansion 을 통해 마지막 식처럼 표현 할 수 있다. 복잡해 보이지만 결국 \((a+b)^2 = a^2+2ab+b^2\) 의 꼴이다. 이때 식의 \(2ab\) 부분은 0이 된다.

\[E_{\mathbf{x}, y, D} \left[ \left( h_{D}(\mathbf{x}) - y \right)^{2} \right] = \underbrace{E_{\mathbf{x}, D} \left[ \left(h_{D}(\mathbf{x}) - \bar{h}(\mathbf{x}) \right)^{2} \right]}_\mathrm{Variance} + E_{\mathbf{x}, y}\left[ \left( \bar{h}(\mathbf{x}) - y \right)^{2} \right]\]

Variance 의 정의 자체가 해당 객체가 평균에서 얼마나 분산되어있는지 이기 때문에, 식의 첫번째 부분을 Variance 라고 할 수 있다. 식의 두번째 부분은 처음에 진행 한 것 처럼 binomial expansion 꼴로 표현하면 아래와 같아진다.

\[E_{\mathbf{x}, y} \left[ \left(\bar{h}(\mathbf{x}) - y \right)^{2}\right] = E_{\mathbf{x}, y} \left[ \left(\bar{h}(\mathbf{x}) -\bar y(\mathbf{x}) )+(\bar y(\mathbf{x}) - y \right)^{2}\right] \\\\ =\underbrace{E_{\mathbf{x}, y} \left[\left(\bar{y}(\mathbf{x}) - y\right)^{2}\right]}_\mathrm{Noise} + \underbrace{E_{\mathbf{x}} \left[\left(\bar{h}(\mathbf{x}) - \bar{y}(\mathbf{x})\right)^{2}\right]}_\mathrm{Bias^2} \\ + 2 \mathrm{\;} E_{\mathbf{x}, y} \left[ \left(\bar{h}(\mathbf{x}) - \bar{y}(\mathbf{x})\right)\left(\bar{y}(\mathbf{x}) - y\right)\right] \label{eq:eq3}\]

동일하게 \(2ab\) 부분은 사라지기 때문에, 최종적으로 expected test error 의 decomposition 은 다음과 같아진다:

\[\underbrace{E_{\mathbf{x}, y, D} \left[\left(h_{D}(\mathbf{x}) - y\right)^{2}\right]}_\mathrm{Expected\;Test\;Error} \\ = \underbrace{E_{\mathbf{x}, D}\left[\left(h_{D}(\mathbf{x}) - \bar{h}(\mathbf{x})\right)^{2}\right]}_\mathrm{Variance} + \underbrace{E_{\mathbf{x}, y}\left[\left(\bar{y}(\mathbf{x}) - y\right)^{2}\right]}_\mathrm{Noise} + \underbrace{E_{\mathbf{x}}\left[\left(\bar{h}(\mathbf{x}) - \bar{y}(\mathbf{x})\right)^{2}\right]}_\mathrm{Bias^2}\]

즉, Bias-Variance decomposition 은 한 머신러닝 알고리즘의 expected test error (혹은 성능) 은 3개의 요인으로 나누어 설명할 수 있음을 의미한다. 한개의 모델이 다른 모델들과 얼마나 다른지를 설명하는 Variance, 전체 모델들의 평균 예측치와 실제값들의 평균의 차를 나타내는 Bias (평균 성능이라고 봐도 무방하다), 그리고 설명할 수 없는 data intrinsic 한 noise 의 합으로 하나의 모델의 성능을 나타낼 수 있다.

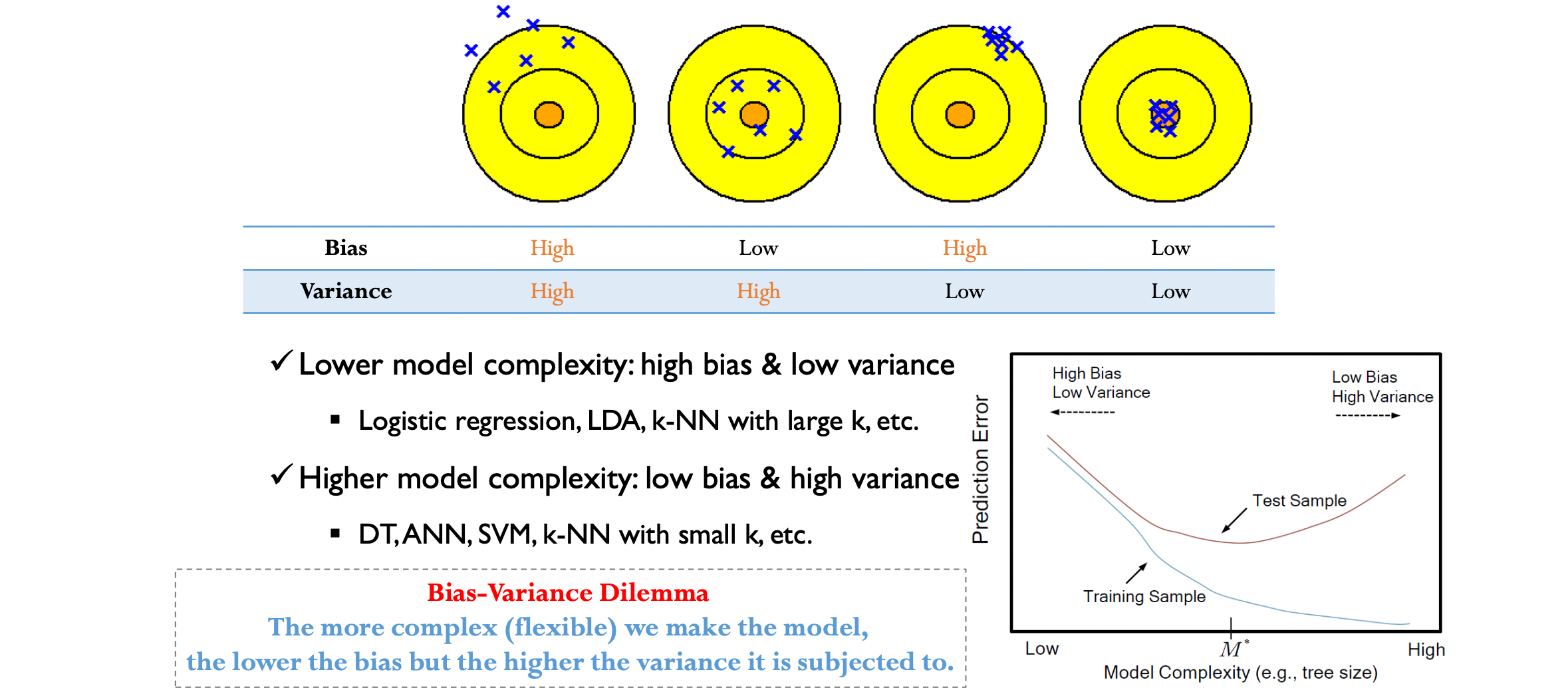
이상적인 알고리즘은 Bias 와 Variance 가 낮지만, 현실적으로 tradeoff 가 발생하기 때문에 필연적으로 둘중 하나는 크다. 보통 Model Compexity 가 낮은 알고리즘들 (ex. LogReg, LDA) 는 High Bias Low Variance 이며, Model Complexity 가 높은 알고리즘들 (ex. NN, Full DT, SVM) 은 Low Bias High Variance 이다.

우측 하단의 그림을 보면 Model complexity 가 높을수록 높은 Variance 를 가졌다는 의미가 와닿는다. Training sample 에 대한 에러율은 0에 수렴하지만, 같은 분포에서 추출한 또다른 데이터셋인 testing sample 에 대한 에러는 굉장히 높다. 이는 데이터셋의 작은 변화에도 모델이 민감하게 반응한다는 것을 의미하며, 자주 접하는 과적합이 해당 모델들의 고질적인 문제를 표현한다.

Low Bias High Variance 를 가진 High complexity 모델들은 과적합에 취약하다는 것은 Bias-Variance Decomposition 에서 수학적으로 증명된 것이다. 그렇기 때문에 Overfitting 에 대한 연구들은 전부 High Variance 를 가진 딥러닝 알고리즘들을 예시로 든다.