Ensemble Learning - Bagging and the Random Forest
Contents
- Ensemble Learning
- Bootstrap Aggregating: Bagging
- Bootstraps
- Result Aggregating
- Majority Voting
- Weighted Voting: (Validation Accuracy)
- Weighted Voting: (Predicted Probability for each class)
- Stacking
- Random Forests
- Variable Importance: OOB
해당 포스트는 2021년 1학기 고려대학교 강필성 교수님의 ‘다변량분석’ 강의를 참고하여 작성되었습니다.
이미지는 강필성 교수님의 강의 슬라이드에서 발췌하였습니다.
A+ 감사했습니다 교수님
Ensemble Learning
이전 장에서 Bias-Variance Tradeoff 에 대해 알아보았다. 머신러닝 알고리즘의 model complexity 가 높다면 보통 Low Bias High Variance 의 특징을 가지며, model complexity 가 낮다면 High Bias Low Variance 의 특징을 갖는다. 둘 중 하나는 본질적으로 높기 때문에, 높은 값을 낮게 만들어주는 앙상블 학습은 크게 Bagging 과 Boosting, 두가지 방법론으로 나뉜다.
Bagging: Decreases Variance
Boosting: Decreases Bias
앙상블 학습의 핵심은 같은 분포에서 추출된 \(N\)개의 데이터셋을 가지고 \(N\)개의 모델을 학습 시킨 뒤, 이 모델들을 적절히 결합하는 것이다.
Bootstrap Aggregating: Bagging
Bootstraps
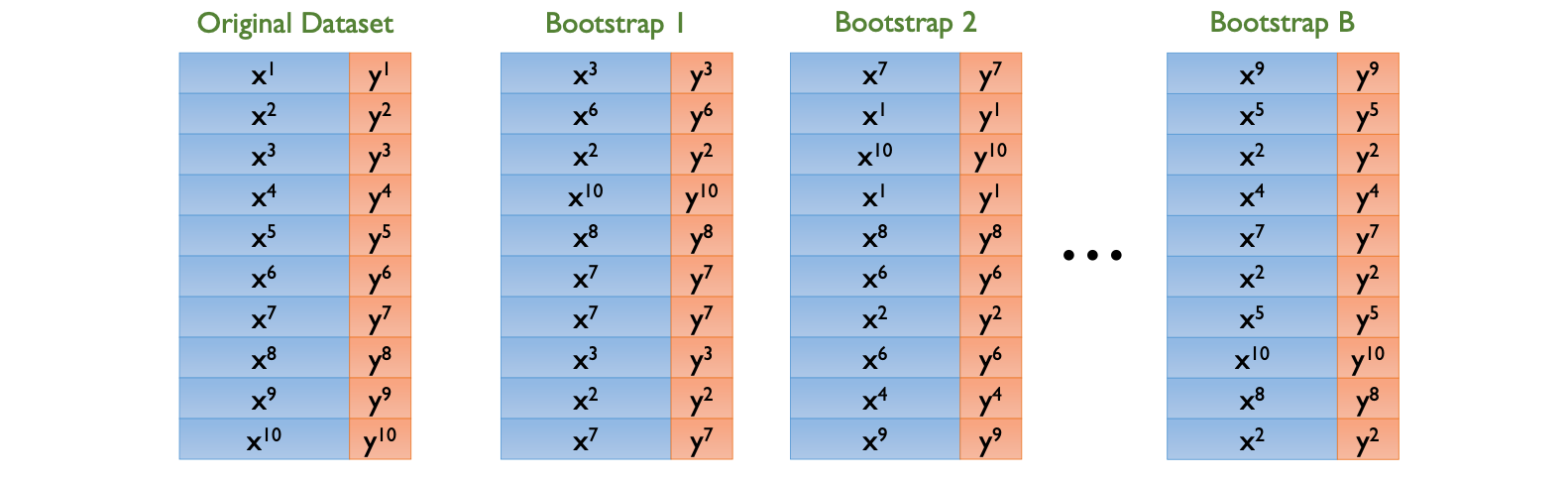
Bagging 은 특정 모델의 분산을 낮춰주는 학습 방법론이다. 위 그림과 같이 기존 데이터셋은 10개의 샘플을 가지고 있다. 이때 기존 데이터셋에서 10개의 샘플을 random 으로 복원추출을 하여 \(B\) 개의 새로운 데이터셋, 즉 Bootstrap 을 생성한다. 해당 Bootstrap 들로 동일한 알고리즘을 학습 한 뒤, 결과를 하나로 합치는 것이 Bagging 의 핵심이다. 이때 알고리즘은 지도학습 알고리즘이면 어떤 것을 사용해도 무방하지만, Bagging 은 앞서 언급하였듯이 high model complexity 를 가진 알고리즘들에 효과적이다. Bagging 자체는 알고리즘이 아니라 앙상블의 다양성을 확보하기 위한 방법론 중 하나이기 때문에, 어떤 알고리즘을 사용하냐에 따라 Bagging with Neural Networks, Bagging with SVM 등으로 불리는 명칭이 달라진다.
Result Aggregating
\(B\) 개의 Bootstrap 으로 \(B\) 개의 모델을 학습시켰다면, 최종적으로 이 모델들을 하나로 합쳐야 한다. Bagging 에서 이 단계를 Result Aggregating 이라 하며, 다양한 방법론들이 있다.
개인적으로 앙상블에서 ‘모델을 Aggregate 한다’ 라는 표현을 싫어한다. 모델을 합치는 단계에선 Classification 하고자 하는 새로운 sample (혹은 test data) 에 대해 각 모델이 각자 예측을 진행하고, 이 결과들을 특정 가중합으로 합쳐 최종 예측값을 뱉어낸다. Black Box 인 모델 ‘자체’ 를 합치는 것이 아니라 개별 모델의 ‘output’ 을 합치는 것이다.
Majority Voting
각 모델의 결과를 합치는 방법론 중 가장 간단한 방법론인 Majority Voting 은, 과반수의 예측값을 최종 예측값으로 선택하는 것이다.
\[\hat y_{Ensemble}=argmax(\sum_{j=1}^n\delta(\hat y_j=i), \ i \in \{0,1\})\]| Ensemble Population | Validation Accuracy | P(y=1) for a test sample | Predicted Class Label |
|---|---|---|---|
| Model 1 | 0.80 | 0.90 | 1 |
| Model 2 | 0.75 | 0.92 | 1 |
| Model 3 | 0.88 | 0.87 | 1 |
| Model 4 | 0.91 | 0.34 | 0 |
| Model 5 | 0.77 | 0.41 | 0 |
| Model 6 | 0.65 | 0.84 | 1 |
| Model 7 | 0.95 | 0.14 | 0 |
| Model 8 | 0.82 | 0.32 | 0 |
| Model 9 | 0.78 | 0.98 | 1 |
| Model 10 | 0.83 | 0.57 | 1 |
위의 예시는 10개의 Bootstrap 을 통해 10개의 Classification 모델을 학습시킨 예시다. 각 모델은 새로 들어온 test sample 에 대해 class 1 에 포함될 확률과, 0.5 로 설정된 cutoff 로 sample 에 대한 최종 예측 class 를 보여준다. 이때 Majority Voting 은 단순히 10개의 모델 중 해당 샘플이 class 1 이라고 예측한 모델의 수가 더 많기 때문에, 해당 샘플에 대한 앙상블의 최종 예측값은 1이 된다.
\[\sum^n_{j=1}\delta (\hat y_j=0) = 4 \\ \sum^n_{j=1}\delta (\hat y_j=1) = 6 \\ \hat y_{Ensemble}=1\]Weighted Voting (Validation Accuracy)
각 모델의 결과에 가중치를 부여해서 합칠 수 있는데, 가중치를 각 모델의 Validation Accuracy 로 설정한 예시는 다음과 같다.
\[\hat y_{Ensemble}=argmax \left( {\sum_{j=1}^n(ValAcc_j) \cdot \delta(\hat y_j=i) \over \sum_{j=1}^n(ValAcc_j)}, \ i \in \{0,1\} \right)\]| Ensemble Population | Validation Accuracy | P(y=1) for a test sample | Predicted Class Label |
|---|---|---|---|
| Model 1 | 0.80 | 0.90 | 1 |
| Model 2 | 0.75 | 0.92 | 1 |
| Model 3 | 0.88 | 0.87 | 1 |
| Model 4 | 0.91 | 0.34 | 0 |
| Model 5 | 0.77 | 0.41 | 0 |
| Model 6 | 0.65 | 0.84 | 1 |
| Model 7 | 0.95 | 0.14 | 0 |
| Model 8 | 0.82 | 0.32 | 0 |
| Model 9 | 0.78 | 0.98 | 1 |
| Model 10 | 0.83 | 0.57 | 1 |
각 모델의 Validation Accuracy 를 \(\delta\) class label 와 곱해준 뒤, Validation Accuracy 의 합으로 나눠줌으로써 정규화를 진행해준다. 이때 \(\delta\) 는 단순한 counting function 이다. 높은 Validation Accuracy 는 모델의 신뢰도가 높다는 것을 의미하기 때문에, 이를 가중치로 반영한 방법론이다.
\[{\sum_{j=1}^n(ValAcc_j) \cdot \delta(\hat y_j=0) \over \sum_{j=1}^n(ValAcc_j)} = 0.424 \\ \\ {\sum_{j=1}^n(ValAcc_j) \cdot \delta(\hat y_j=1) \over \sum_{j=1}^n(ValAcc_j)} = 0.576 \\ \\ \hat y_{Ensemble} = 1\]Weighted Voting (Predicted Probability for each class)
가중치를 각 모델의 클래스 예측확률로 사용한 예시는 다음과 같다.
\[\hat y_{Ensemble}=argmax \left({1 \over n} \sum_{j=1}^n P(y=i), \ i \in \{0,1\} \right)\]| Ensemble Population | Validation Accuracy | P(y=1) for a test sample | Predicted Class Label |
|---|---|---|---|
| Model 1 | 0.80 | 0.90 | 1 |
| Model 2 | 0.75 | 0.92 | 1 |
| Model 3 | 0.88 | 0.87 | 1 |
| Model 4 | 0.91 | 0.34 | 0 |
| Model 5 | 0.77 | 0.41 | 0 |
| Model 6 | 0.65 | 0.84 | 1 |
| Model 7 | 0.95 | 0.14 | 0 |
| Model 8 | 0.82 | 0.32 | 0 |
| Model 9 | 0.78 | 0.98 | 1 |
| Model 10 | 0.83 | 0.57 | 1 |
앞선 예시들과 같이 개별 모델을 설명하는 값을 가중치로 적절히 이용할 수 있다. Validation Accuracy 와 각 클래스 예측확률을 적절히 조합한 가중치 또한 가능하다.
Stacking
Result Aggregating 중 가장 높은 성능을 내는 방법론 중 하나인 Stacking 은 앞선 weighted voting 과는 조금 다른 approach 를 이용한다.
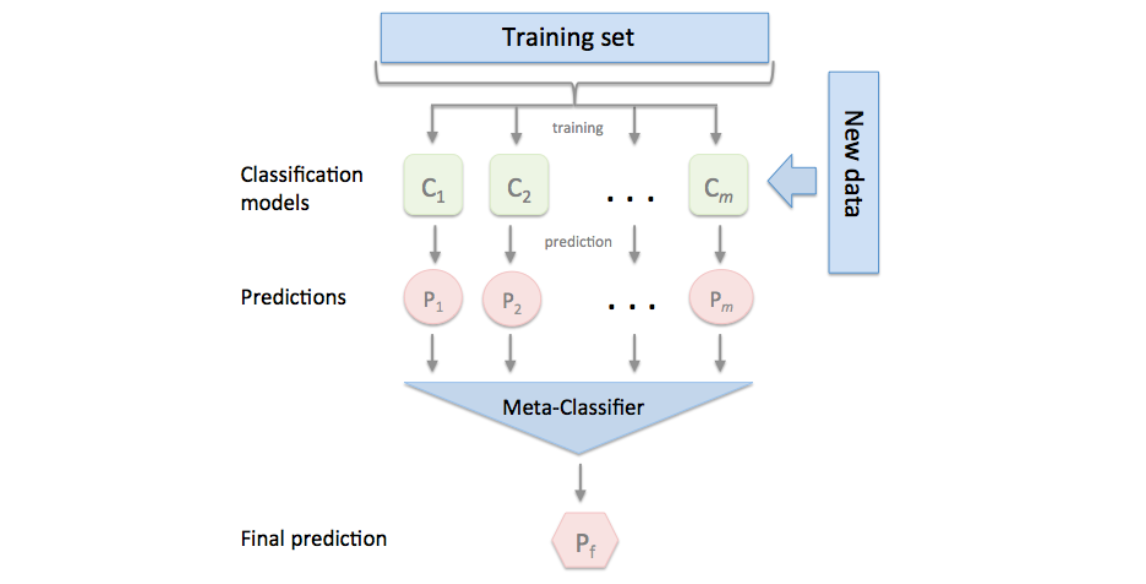
Bootstrap 으로 각 모델을 생성한 뒤, 새로운 샘플에 대한 예측치를 다시 입력치 \(\mathbf{x}\) 로, 실제 정답을 \(y\) 로 갖는 새로운 Meta-Classifier 을 학습하는 방법론이다.
Random Forests
사실 Bagging 은 굉장히 직관적인 앙상블 기법이다. 복원추출로 동일한 샘플수를 가진 bootstrap 을 생성하고, 모델들을 학습시킨 뒤 적절히 결합하여 complex 모델의 분산을 줄인다. High complexity 를 가진 그 어떤 모델에 bagging 을 적용할 수 있고, base learner (기준이 되는 학습 알고리즘) 에 따라 bagging with SVM 등으로 불린다. 반면 Random Forest 는 의사결정나무에 bagging 을 적용한 모델로, 특별히 혼자 다르게 불리는 이유는 OOB 데이터셋에 의한 추가적인 insight 도출 능력과 bagging 에 있어 모든 설명변수를 사용하지 않는다는 특징이 있기 때문이다.

Random Forest 는 이름에서 알 수 있듯이 의사결정나무의 앙상블 모델이다. 기존 Bagging 을 사용하지만, Bootstrap 을 이용한 학습 단계에서 모든 설명변수를 사용하지 않고 random 한 설명변수의 subset 만으로 학습을 진행한다는 특징을 가지고 있다.
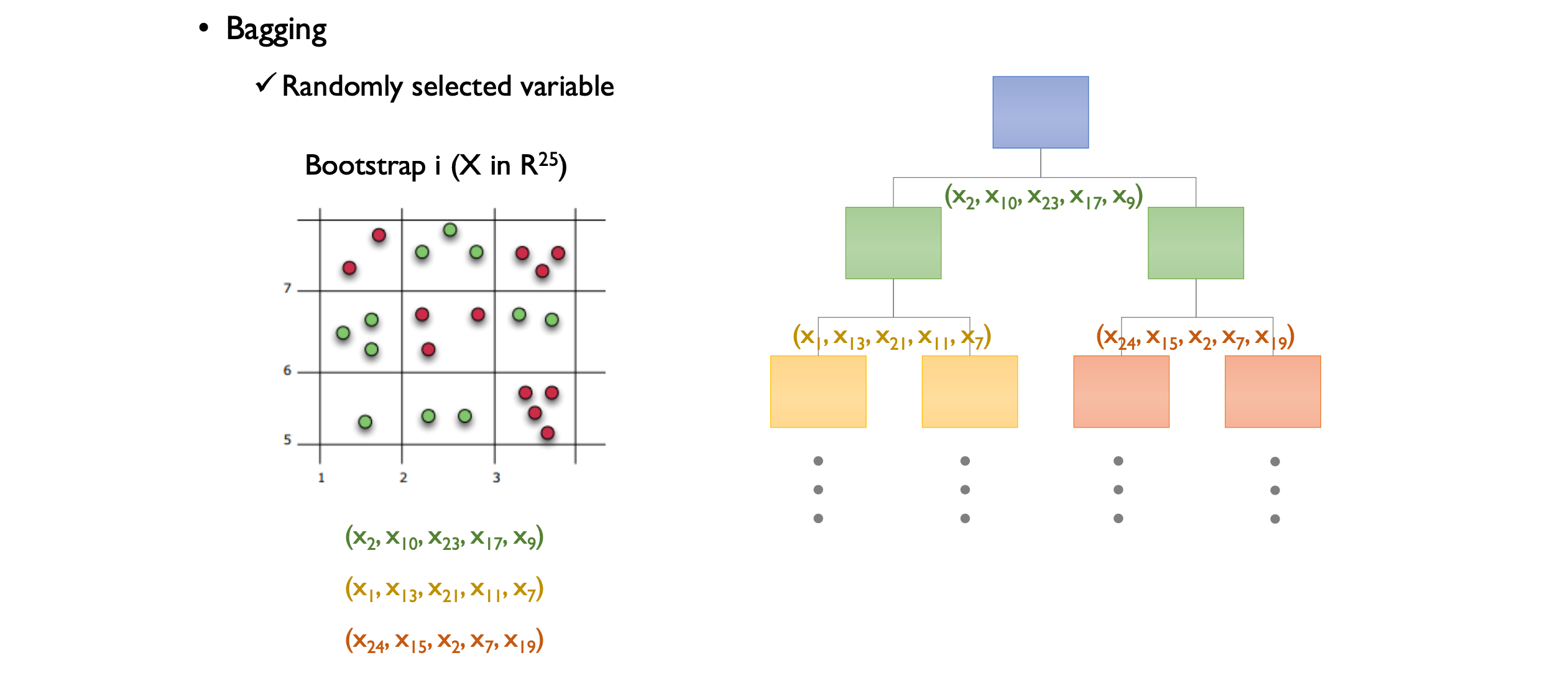
위 예시는 25개의 설명변수를 가진 데이터셋에서 Bagging 을 진행 한 뒤, 학습을 진행했을 때 사용된 설명변수를 나타낸다. 첫번째 split 에선 \(x_2, x_{10},x_{23}, x_{17}, x_{9}\) 설명변수들로만 split 을 진행했고, 그다음 split 에선 또 다른 설명변수의 random subset 이 사용된 걸 볼 수 있다. 이러한 과정으로 통해 Random Forest 는 Bagging 으로 다양성 확보를 하고, 설명변수를 random 하게 추출함으로써 다양성을 추가적으로 더 확보할 수 있다.
Split 을 할때 설명변수를 random 하게 추출하지 않고 때 전부 사용한다면 만들어진 bagging tree 들은 성능이 서로 비슷하다. 하지만 random 추출을 했기 때문에 만들어진 tree 들은 성능이 서로 굉장히 다르다. 비록 개별 성능은 설명변수를 전부 사용한 개별 tree 들 보다 떨어지지만, 합치면 다양성을 보다 확보하면서 성능까지 챙길 수 있다.
강필성 교수님께선 이를 ‘2보 전진을 위한 1보 후퇴’ 라고 표현하셨으며, Random Forest 를 관통하는 개념이다.
Variable Importance: OOB
K-fold data split 과는 달리 Bagging 은 각 bootstrap 을 만들때 복원추출을 한다. 그렇기에 bootstrap 수가 아무리 많아도, 확률적으로 단 한번도 bootstrap 에 포함되지 않는 샘플들이 있기 마련이다. 이를 OOB Data (Out-of-bag) 라고 하며, 앙상블의 개별 모델의 Validation Set 으로 쓰인다. 통상적인 머신러닝 모델을 학습시킬 때 데이터셋을 Train/Validation/Test set 으로 나누어 학습을 진행하지만, OOB의 존재 덕분에 따로 Validation Set 을 빼놓지 않고 보다 더 많은 Training sample 을 쓸 수 있다는 장점이 있다.
앙상블 모델중에서 Random Forest 는 실무에서 활용도가 굉장히 높은 모델이다. 바로 OOB Data 로 설명변수의 중요도를 구할 수 있기 때문이다.
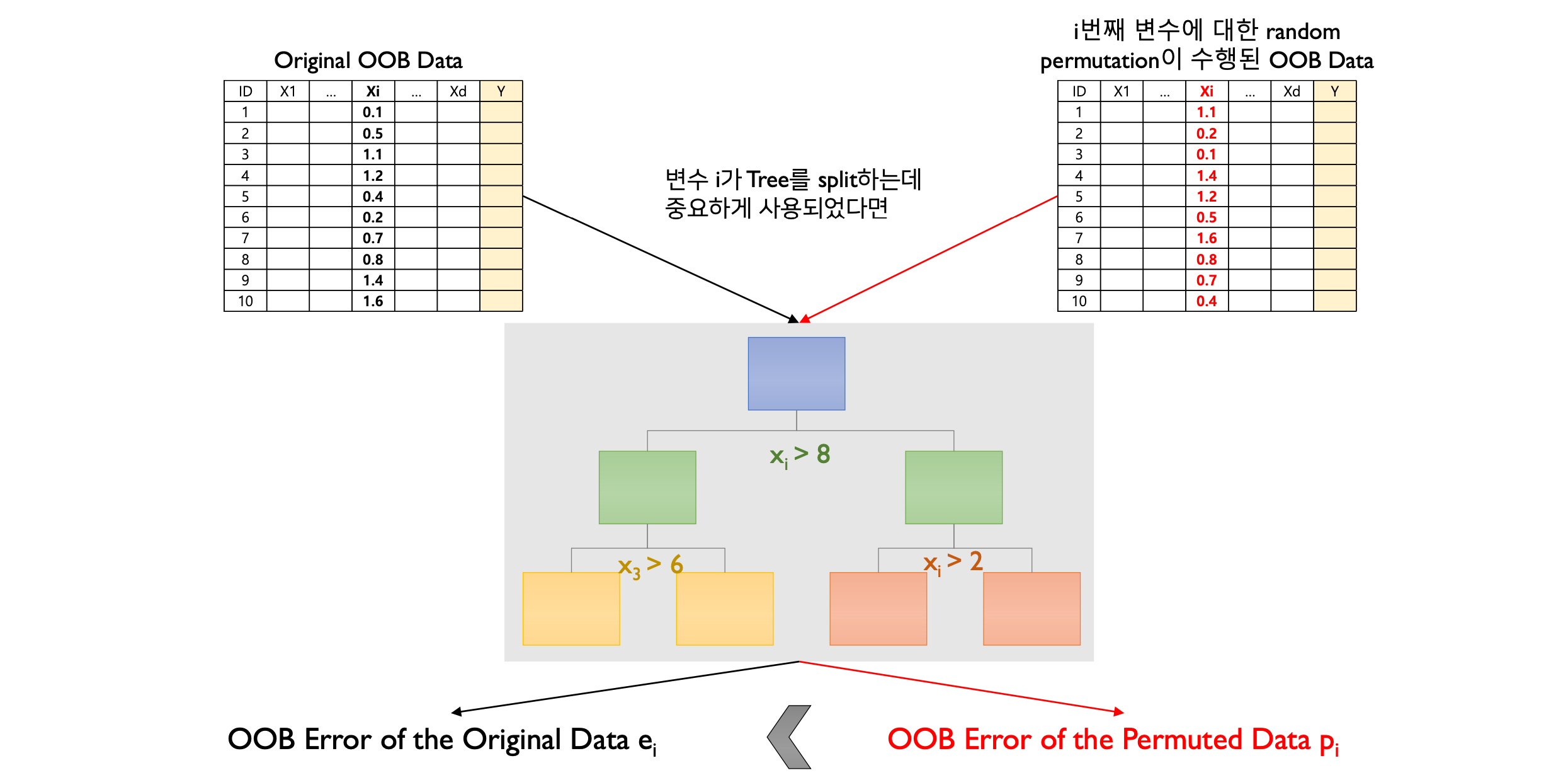
Step 1: Population (앙상블을 구성하는 개별 모델) 에 대해 OOB error (\(e_i\)) 를 계산한다.
Step 2: 중요도를 구하고자 하는 설명변수 \(x_i\) 의 값들에 대해 permutation 을 진행 후, permutated OOB error (\(p_i\)) 를 계산한다.
Step 3: Population 에 대해 \(p_i - e_i\) 의 평균과 분산을 구한 뒤, 변수의 중요도를 산출한다.
이때 Step 2 의 permutation 은 해당 변수에 대한 sample 의 값을 random 하게 섞는 것을 의미한다. 만약 Random Forest 에서 변수 \(x_i\) 의 중요도가 높다면, \(p_i - e_i\) 의 값은 커야 하며 편차가 적어야 한다.
\[d_i^m = p_i^m - e_i^m \\ \bar d_i = {1\over m}\sum_{i=1}^m d_i^m \\ s_i^2 = {1 \over m-1} \sum_{i=1}^m (d_i^m - \bar d_i)^2 \\ v_i = {\bar d_i \over s_i}\]\(d_i^m\) 은 m 번째 tree 에서 설명변수 i 에 대해 permutation 전후 OOB error 의 차이를 나타내고, 이에 따른 평균을 분자로, 분산을 분모로 두어 변수의 중요도 \(v_i\) 를 구할 수 있다.