Ensemble Learning - Adaptive Boosting

July 06, 2022

2022   ·   machine-learning  

Contents

  • Adaptive Boosting
  • AdaBoost: Algorithm

해당 포스트는 2021년 1학기 고려대학교 강필성 교수님의 ‘다변량분석’ 강의를 참고하여 작성되었습니다.

이미지는 강필성 교수님의 강의 슬라이드에서 발췌하였습니다.

A+ 감사했습니다 교수님

Adaptive Boosting

이전 장에서 살펴본 Bagging 은 bootstrap 을 만들어 high model complexity 를 가진 모델을 학습시킨 뒤, 적절히 결합하는 앙상블 방법론이다. Boosting 은 반대로 하나의 데이터셋에 하나의 모델을 학습시킨 후, 풀어내지 못한 것에 대해 다음단계에서 중점적으로 학습을 반복하는 방법론이다.

Boosting 에선 Strong vs. Weak model 이란 개념이 등장한다. Classifier 기준으로, Weak model 은 random guessing 보다 성능이 아주 약간 좋은 모델을 의미하며, boosting 은 이런 Weak model 을 기준으로 Strong model 을 향해 나아간다. Boosting 은 데이터셋을 통해 성능이 아주 낮은 weak model 을 먼저 학습시킨 뒤, 오분류한 데이터셋 속 샘플에 대해 가중치를 부여하고 새로운 모델의 학습을 반복한다. 이렇기 때문에 bagging 과는 달리 병렬연산이 불가능하다.

Bagging 은 병렬처리가 가능하고, Boosting 은 병렬처리가 불가능하지만 실제로는 Boosting 의 학습이 훨씬 빠른 경우를 종종 볼 수 있다. Bagging 은 애초에 High complexity 를 가진 모델을 병렬 연산하는 것이고, Boosting 은 Weak model 을 직렬연산하는 것이다. 하지만 오히려 Weak model 의 직렬연산이 Bagging 의 high complexity 모델 하나를 학습시키는것보다 빠른 경우가 많다.

Adaptive boosting 은 Boosting 방법론 중 weak model 을 stump tree 로 사용하는 앙상블 방법론이다. Stump tree 란 decision boundary split 을 단 1번만 진행한 Decision tree 를 의미하며, (제대로 학습이 이루어졌다고 가정하면) random guessing 보다 성능이 약간 좋다는 특징을 가진다.

AdaBoost: Algorithm

  1. AdaBoost 의 지정 hyperparameter \(T\) 는 individual learner 의 개수를 의미한다. AdaBoost 는 직렬연산을 기반한 알고리즘이기 때문에, individual learner 의 개수는 곧 알고리즘의 iteration 을 의미한다. 보통 50~100개를 지정한다.

  2. AdaBoost 의 Input 은 \(N\) 개의 정답 pair 을 가진 학습 데이터셋 \(S\) 다. 이때 주목할만한 점은 정답라벨 \(y_i\) 다. 일반적인 Classification 을 수행하기 위해 데이터셋의 정답라벨은 \(0,1\) 의 값을 갖는데 AdaBoost 의 특성상 \(-1, 1\) 을 사용한다. 예측하는데 있어 아무런 차이가 없지만, 이렇게 값을 바꾸어 사용하는 이유는 weight update 에서 확인 할 수 있다.

  3. \(D_1(i)\) 는 1번째 iteration 에서 sample \(i\) 가 선택될 확률분포를 의미한다. 알고리즘 초기엔 일양분포를 사용함으로써 \(i\) 가 선택될 확률은 다른 sample 들과 동일하지만, iteration 이 진행되며 이 분포는 바뀐다.

  4. for loop 을 이용해서 individual learner 의 개수만큼 알고리즘을 반복한다.

    1. 확률분포 \(D_t\) 를 이용하여 모델 \(h_t\) 를 학습시킨다. 여기서 주목할 점은 AdaBoost 의 학습용 데이터셋 생성은 Boosting 과 마찬가지로 복원추출을 사용하지만, 첫번째 iteration 에서만 복원추출하는 방식이 Uniform distribution 이기 때문에 random 하다. 이때 \(h_t\) 는 Stump tree 를 의미한다.

    2. 오분류율인 \(\epsilon_t = P_{D_t}(h_t(x)\neq y)\) 을 계산한다.

    3. 오분류율 \(\epsilon_t \geq 0.5\) 면 알고리즘을 종료하고 다시 처음부터 시작한다. 학습한 모델은 weak model 인 stump tree 이기 때문에, 아무리 성능이 낮을지언정 random guessing 보다 성능이 좋아야 한다. 오분류율이 0.5 보다 크거나 같다는 의미는 stump tree 가 random guessing 보다 못했다는 것을 의미하기 때문에, 처음부터 다시 해보라는 일종의 장치를 걸어둔 것이다.

    4. \(\alpha_t = {1\over2}ln({1-\epsilon_t \over \epsilon_t})\) 를 계산하여 가중치 \(\alpha_t\) 를 구한다.
    5. \(D_{t+1}(i)= {D_t(i)\mathbf{exp}(-\alpha_t y_i h_t (x_i))\over Z_t}\) 를 통해 다음 iteration 의 샘플들이 선택되는 확률분포를 update 한다. 이 부분을 통해 다음 iteration 에서 샘플들이 복원추출로 선택되는 확률이 달라지는 것이다. \(Z_t\) 는 정규화 factor 이다.

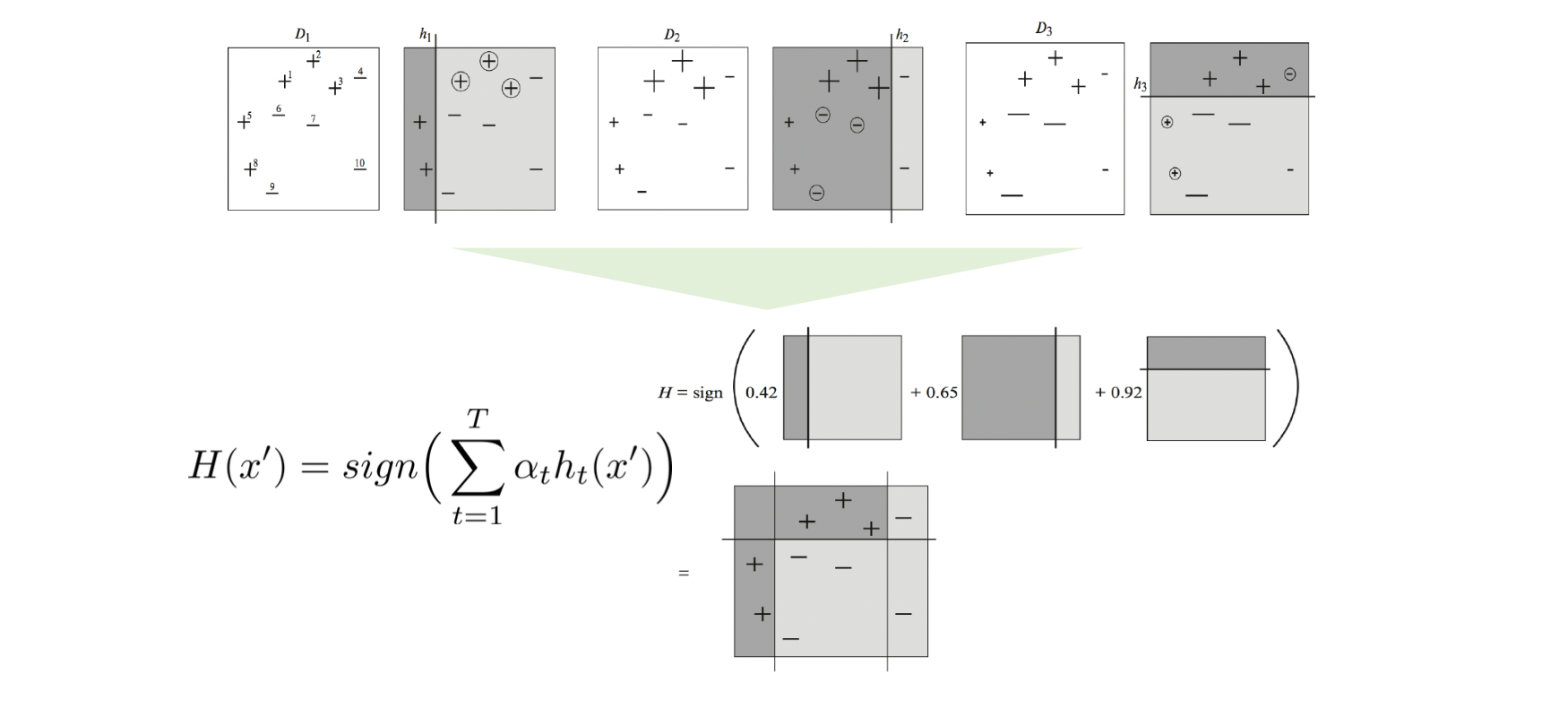
  5. \(T\) 만큼의 iteration 이 종료되면, 모든 모델 \(h_t\) 와 이에 대한 \(\alpha_t\) 값을 더한 뒤, testing sample \((x',y')\) 를 넣어 모델을 검증한다.

\[D_{t+1}(i)= {D_t(i)\mathbf{exp}(-\alpha_t y_i h_t (x_i))\over Z_t}\]

AdaBoost 의 핵심은 \(D_t\) 의 계산에서 볼 수 있다.

먼저, \(D_t(i)\) 는 \(t\) 시점에서 샘플 \(i\) 가 선택될 확률을 의미한다.

\(\alpha_t\) 의 계산식 \({1\over2}ln({1-\epsilon_t \over \epsilon_t})\) 를 보면 오분류율에 따라 계산이 되기 때문에, 모델의 정확도가 높을수록 \(\alpha_t\) 가 크다.

데이터셋의 정답라벨을 왜 \(y_i \in \{-1,1\}\) 으로 설정해야하는지는 \(y_i h_t (x_i)\) 의 작동 원리때문이다. \(y_i\) 는 샘플 \(i\)의 정답라벨이고, \(h_t(x_i)\) 는 stump tree 의 예측값이다. 만약 샘플 \(i\) 에 대해 모델이 올바르게 예측했다면 \(y_i h_t (x_i)\) 는 1이 될것이고, 올바르게 예측을 못했다면 \(y_i h_t (x_i)\) 는 -1 이 될것이다.

그렇기에 \(\mathbf{exp}(-\alpha_t y_i h_t (x_i))\) 는 \(h_t\) 가 성능이 높고 샘플 \(i\) 를 올바르게 예측했다면 \(i\) 가 선택될 확률을 줄이는 것이고, \(h_t\) 가 정확한 모델임에도 불구하고 \(i\) 를 올바르게 예측을 못했다면 \(i\) 가 선택될 확률을 다음 단계에서 높히는 것을 의미한다. 이때 \(i\) 가 선택될 확률, 즉 증가/감소 폭은 모델의 성능인 가중치 \(\alpha_t\) 에 의해 결정된다.

AdaBoost 는 위와 같은 알고리즘으로 이전단계에 분류를 잘 못한 샘플에 대해 복원추출에서 선택될 확률을 높힘으로써, 모델의 성능을 확보한다.

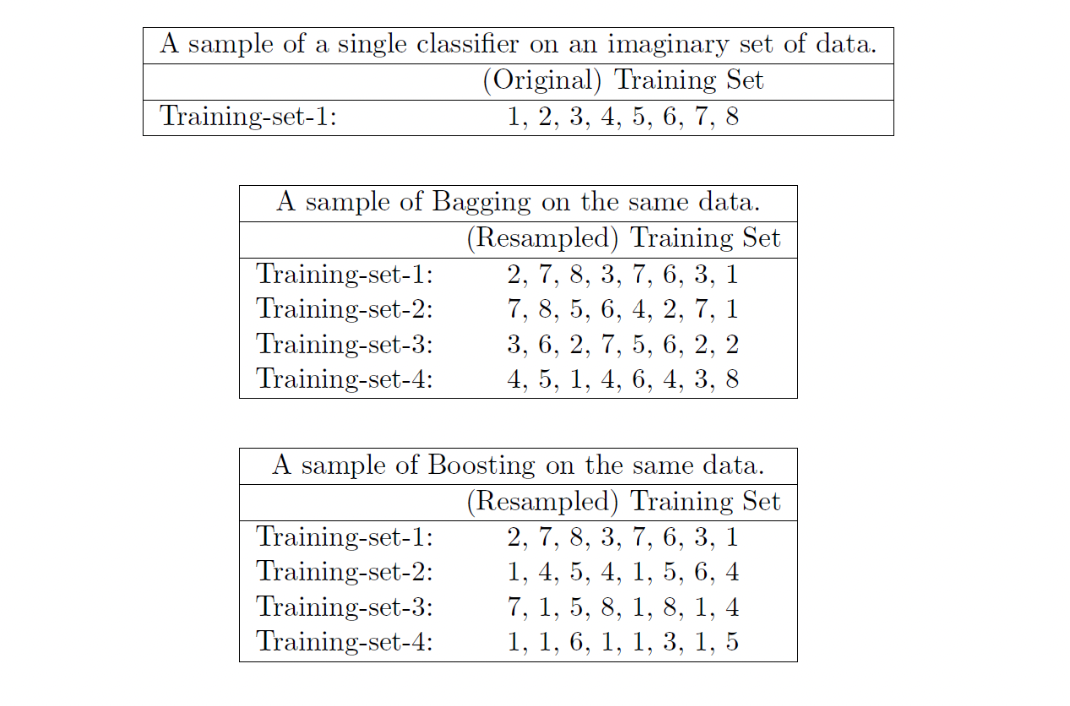
위 그림을 보면 Bagging 에서 각 Bootstrap 마다 선택되는 샘플들과 Boosting 의 iteration 마다 선택되는 샘플들을 비교할 수 있다. Bagging 에선 모든 샘플들이 random 하게 복원추출이 되는 반면, Boosting 에선 4번째 iteration 을 위해 추출된 데이터에선 1이 이전 단계보다 훨씬 많이 등장하는 것을 볼 수 있다.